2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.[2023.山东枣庄第三中学高二月考]在空间直角坐标系中,定义:平面α的一般方程为Ax+By+Cz+
D=0(A,B,C,D∈R,A²+B²+C²²≠0),点P(xo,yo,z0)到平面α的距离d=$\frac{IAx。+By。+Cz+D1}{\sqrt{A²+B²+C²}}$,则在底面边长与高都为2的正四棱锥中,底面中心0到侧面的距离等于________.
D=0(A,B,C,D∈R,A²+B²+C²²≠0),点P(xo,yo,z0)到平面α的距离d=$\frac{IAx。+By。+Cz+D1}{\sqrt{A²+B²+C²}}$,则在底面边长与高都为2的正四棱锥中,底面中心0到侧面的距离等于________.
答案:
$\frac {2\sqrt {5}}{5}$
2.[2023.陕西宝鸡中学高二月
考]若点M在平面α外,过点
M作平面α的垂线,则称垂足
N为点M在平面α内的正投
影,记为N=f;(M).如图,在棱
长为1的正方体ABCD−A,BC,D,中,记平面
AB,C,D为β,平面ABCD为γ,点P是棱CC,上一动点(与C,C,不重合),Q=£(f(P)),Q2=
f(∮,(P)).给出下列三个结论:
①线段PQ2长度的取值范围是$\frac{1}{2}$$\frac{\sqrt{2}}{2}$;
②存在点P使得PQ,//平面β;
③存在点P使得PQ⊥PQ2.
其中正确结论的序号是________.

考]若点M在平面α外,过点
M作平面α的垂线,则称垂足
N为点M在平面α内的正投
影,记为N=f;(M).如图,在棱
长为1的正方体ABCD−A,BC,D,中,记平面
AB,C,D为β,平面ABCD为γ,点P是棱CC,上一动点(与C,C,不重合),Q=£(f(P)),Q2=
f(∮,(P)).给出下列三个结论:
①线段PQ2长度的取值范围是$\frac{1}{2}$$\frac{\sqrt{2}}{2}$;
②存在点P使得PQ,//平面β;
③存在点P使得PQ⊥PQ2.
其中正确结论的序号是________.

答案:
①②
3.[2022.海南高三模拟预测]海口钟
楼的历史悠久,最早是为适应对外
通商而建立,已成为海口的最重要
的标志性与象征性建筑物之一,如
图所示,海口钟楼的主体结构可以看成一个长方体,四个侧面各有一个大钟,则从8:00到10:00 这段时间内,相邻两面钟的分针所成角为60°的次数为 ( )

A.2
B.4
C.6
D.8
楼的历史悠久,最早是为适应对外
通商而建立,已成为海口的最重要
的标志性与象征性建筑物之一,如
图所示,海口钟楼的主体结构可以看成一个长方体,四个侧面各有一个大钟,则从8:00到10:00 这段时间内,相邻两面钟的分针所成角为60°的次数为 ( )

A.2
B.4
C.6
D.8
答案:
D
4.[2023.湖北襄阳四中高二期中]在2021年6月17 日,神舟十二号载人飞船顺利升空并于6.5h后
新定义、新情境问题 ?答案见D29
与天和核心舱成功对接.图(1)是神舟十二号飞船推进舱及其推进器的简化示意图,半径相等的圆I1,12,I3,14与圆柱001的底面分别相切于A,
B,C,D四点,且圆I与圆I2,圆I2与圆1,圆1与圆I4,圆互与圆I1分别外切,线段A,A为圆柱00,的母线,点M为线段AO的中点,点N在线段
CO,上,且CN=2NO.已知圆柱0O,的底面半径为2,AA=4.
(1)求证:AM//平面BDN.
(2)线段AA,上是否存在一点E,使得OE⊥平面
BDN?若存在,请求出AE的长;若不存在,请说明理由.
(3)图(2)是飞船推进舱与即将对接的天和核心舱的相对位置的简化示意图.天和核心舱是底面半径为2的圆柱0203,它与飞船推进舱共轴,即0,0,02,03共线.核心舱体两侧伸展出太阳翼,其中三角形RST是以RS为斜边的等腰直角三角形,四边形PQRS为矩形.已知推进舱与核心舱的距离为4,即0,02=4,且0203=RS=2,PS=7.在对接过程中,核心舱相对于推进舱可能会相对作出逆时针旋转的运动,请你求出在舱体相对距离不变的情况下,在舱体相对旋转过程中,直线A1P 与平面PQRS所成角的正弦值的最大值.
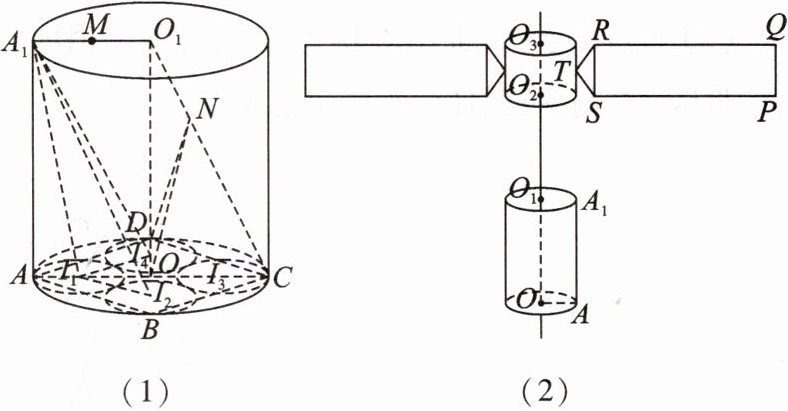
新定义、新情境问题 ?答案见D29
与天和核心舱成功对接.图(1)是神舟十二号飞船推进舱及其推进器的简化示意图,半径相等的圆I1,12,I3,14与圆柱001的底面分别相切于A,
B,C,D四点,且圆I与圆I2,圆I2与圆1,圆1与圆I4,圆互与圆I1分别外切,线段A,A为圆柱00,的母线,点M为线段AO的中点,点N在线段
CO,上,且CN=2NO.已知圆柱0O,的底面半径为2,AA=4.
(1)求证:AM//平面BDN.
(2)线段AA,上是否存在一点E,使得OE⊥平面
BDN?若存在,请求出AE的长;若不存在,请说明理由.
(3)图(2)是飞船推进舱与即将对接的天和核心舱的相对位置的简化示意图.天和核心舱是底面半径为2的圆柱0203,它与飞船推进舱共轴,即0,0,02,03共线.核心舱体两侧伸展出太阳翼,其中三角形RST是以RS为斜边的等腰直角三角形,四边形PQRS为矩形.已知推进舱与核心舱的距离为4,即0,02=4,且0203=RS=2,PS=7.在对接过程中,核心舱相对于推进舱可能会相对作出逆时针旋转的运动,请你求出在舱体相对距离不变的情况下,在舱体相对旋转过程中,直线A1P 与平面PQRS所成角的正弦值的最大值.

答案:
思维路径:
(1)从原图中抽出部分图形,并取$AO$的中点$M'$→证明四边形$AMO_{1}M'$是平行四边形→$AM\parallel O_{1}M'$→再证明$ON\parallel M'O_{1}$→$AM\parallel ON$→证明$AM\parallel$平面$BDN$。
(2)建立空间直角坐标系并设$E(2,0,t)(0\leqslant t\leqslant4)$→$OE\perp$平面$BDN$→$\overrightarrow{OE}\cdot\overrightarrow{DB}=0$,$\overrightarrow{OE}\cdot\overrightarrow{DN}=0$→求出$t$→存在。
(3)不妨设$A_{1}$顺时针旋转$\alpha(\alpha\gt0)$,得出各点坐标→由线面角的向量法求得$A_{1}P$与平面$PQRS$所成的角的正弦值$\sin\theta$→利用换元法、基本不等式求得最大值。
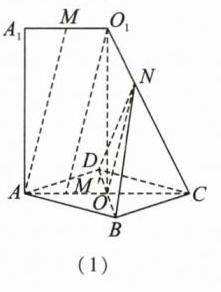
(1)【证明】图
(1)是从原图中抽出的部分图形,取$AO$的中点$M'$。 又$M$是$A_{1}O_{1}$的中点, 则$MO_{1}\parallel AM'$且$MO_{1}=AM'$, 所以四边形$AMO_{1}M'$是平行四边形, 所以$AM\parallel O_{1}M'$。 又$OM' = 1$,$OC = 2$,所以$\frac{OC}{OM'}=2$。 又$\frac{CN}{NO_{1}}=2$,所以$ON\parallel M'O_{1}$, 所以$AM\parallel ON$。 因为$AM\not\subset$平面$BDN$,$ON\subset$平面$BDN$, 所以$AM\parallel$平面$BDN$。
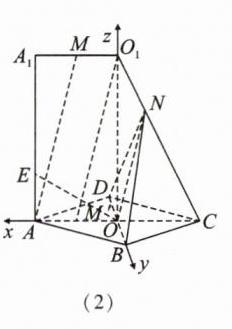
(2)【解】以$O$为原点,分别以$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OO_{1}}$所在方向为$x$轴、$y$轴、$z$轴的正方向建立空间直角坐标系,如图
(2),则$O(0,0,0)$,$B(0,2,0)$,$D(0,-2,0)$,$N(-\frac{2}{3},0,\frac{8}{3})$。 所以$\overrightarrow{DB}=(0,4,0)$,$\overrightarrow{DN}=(-\frac{2}{3},2,\frac{8}{3})$。 设$E(2,0,t)(0\leqslant t\leqslant4)$,则$\overrightarrow{OE}=(2,0,t)$。 若$OE\perp$平面$BDN$,则$\begin{cases}\overrightarrow{OE}\cdot\overrightarrow{DB}=0\\\overrightarrow{OE}\cdot\overrightarrow{DN}=0\end{cases}$, 即$-\frac{4}{3}+\frac{8}{3}t = 0$,解得$t=\frac{1}{2}$,即$AE=\frac{1}{2}$时,$OE\perp$平面$BDN$。
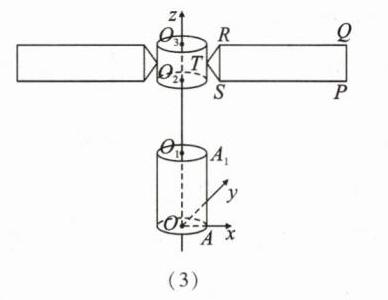
(3)【解】在图
(3)的坐标系下,将矩形$PQRS$作为参照物,不妨设$A_{1}$顺时针旋转$\alpha(\alpha\gt0)$, 则$A_{1}(2\cos(-\alpha),2\sin(-\alpha),4)$,即$A_{1}(2\cos\alpha,-2\sin\alpha,4)$,$P(10,0,8)$, 所以$\overrightarrow{A_{1}P}=(10 - 2\cos\alpha,2\sin\alpha,4)$。 因为$y$轴与平面$PQRS$垂直, 所以平面$PQRS$的一个法向量为$\boldsymbol{u}=(0,1,0)$。 设$A_{1}P$与平面$PQRS$所成的角为$\theta$, 则$\sin\theta=|\cos\langle\overrightarrow{A_{1}P},\boldsymbol{u}\rangle|=\frac{|\overrightarrow{A_{1}P}\cdot\boldsymbol{u}|}{|\overrightarrow{A_{1}P}||\boldsymbol{u}|}=\frac{|2\sin\alpha|}{\sqrt{(10 - 2\cos\alpha)^{2}+4\sin^{2}\alpha + 16}}=\frac{1}{\sqrt{10}}\cdot\sqrt{\frac{1-\cos^{2}\alpha}{3-\cos\alpha}}$。 若$\cos\alpha=\pm1$,则$\sin\theta = 0$; 若$-1\lt\cos\alpha\lt1$,令$t = 3-\cos\alpha\in(2,4)$,则$1-\cos^{2}\alpha=-8 + 6t - t^{2}$, 所以$\sin\theta=\frac{1}{\sqrt{10}}\cdot\sqrt{-(t+\frac{8}{t})+6}\leqslant\frac{1}{\sqrt{10}}\cdot\sqrt{-4\sqrt{2}+6}=\frac{\sqrt{10}-\sqrt{5}}{5}$, 当且仅当$t=\frac{8}{t}$,即$t = 2\sqrt{2}$,亦即$\cos\alpha=3 - 2\sqrt{2}$时,$\sin\theta$取得最大值$\frac{\sqrt{10}-\sqrt{5}}{5}$。
思维路径:
(1)从原图中抽出部分图形,并取$AO$的中点$M'$→证明四边形$AMO_{1}M'$是平行四边形→$AM\parallel O_{1}M'$→再证明$ON\parallel M'O_{1}$→$AM\parallel ON$→证明$AM\parallel$平面$BDN$。
(2)建立空间直角坐标系并设$E(2,0,t)(0\leqslant t\leqslant4)$→$OE\perp$平面$BDN$→$\overrightarrow{OE}\cdot\overrightarrow{DB}=0$,$\overrightarrow{OE}\cdot\overrightarrow{DN}=0$→求出$t$→存在。
(3)不妨设$A_{1}$顺时针旋转$\alpha(\alpha\gt0)$,得出各点坐标→由线面角的向量法求得$A_{1}P$与平面$PQRS$所成的角的正弦值$\sin\theta$→利用换元法、基本不等式求得最大值。
(1)【证明】图
(1)是从原图中抽出的部分图形,取$AO$的中点$M'$。 又$M$是$A_{1}O_{1}$的中点, 则$MO_{1}\parallel AM'$且$MO_{1}=AM'$, 所以四边形$AMO_{1}M'$是平行四边形, 所以$AM\parallel O_{1}M'$。 又$OM' = 1$,$OC = 2$,所以$\frac{OC}{OM'}=2$。 又$\frac{CN}{NO_{1}}=2$,所以$ON\parallel M'O_{1}$, 所以$AM\parallel ON$。 因为$AM\not\subset$平面$BDN$,$ON\subset$平面$BDN$, 所以$AM\parallel$平面$BDN$。
(2)【解】以$O$为原点,分别以$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OO_{1}}$所在方向为$x$轴、$y$轴、$z$轴的正方向建立空间直角坐标系,如图
(2),则$O(0,0,0)$,$B(0,2,0)$,$D(0,-2,0)$,$N(-\frac{2}{3},0,\frac{8}{3})$。 所以$\overrightarrow{DB}=(0,4,0)$,$\overrightarrow{DN}=(-\frac{2}{3},2,\frac{8}{3})$。 设$E(2,0,t)(0\leqslant t\leqslant4)$,则$\overrightarrow{OE}=(2,0,t)$。 若$OE\perp$平面$BDN$,则$\begin{cases}\overrightarrow{OE}\cdot\overrightarrow{DB}=0\\\overrightarrow{OE}\cdot\overrightarrow{DN}=0\end{cases}$, 即$-\frac{4}{3}+\frac{8}{3}t = 0$,解得$t=\frac{1}{2}$,即$AE=\frac{1}{2}$时,$OE\perp$平面$BDN$。
(3)【解】在图
(3)的坐标系下,将矩形$PQRS$作为参照物,不妨设$A_{1}$顺时针旋转$\alpha(\alpha\gt0)$, 则$A_{1}(2\cos(-\alpha),2\sin(-\alpha),4)$,即$A_{1}(2\cos\alpha,-2\sin\alpha,4)$,$P(10,0,8)$, 所以$\overrightarrow{A_{1}P}=(10 - 2\cos\alpha,2\sin\alpha,4)$。 因为$y$轴与平面$PQRS$垂直, 所以平面$PQRS$的一个法向量为$\boldsymbol{u}=(0,1,0)$。 设$A_{1}P$与平面$PQRS$所成的角为$\theta$, 则$\sin\theta=|\cos\langle\overrightarrow{A_{1}P},\boldsymbol{u}\rangle|=\frac{|\overrightarrow{A_{1}P}\cdot\boldsymbol{u}|}{|\overrightarrow{A_{1}P}||\boldsymbol{u}|}=\frac{|2\sin\alpha|}{\sqrt{(10 - 2\cos\alpha)^{2}+4\sin^{2}\alpha + 16}}=\frac{1}{\sqrt{10}}\cdot\sqrt{\frac{1-\cos^{2}\alpha}{3-\cos\alpha}}$。 若$\cos\alpha=\pm1$,则$\sin\theta = 0$; 若$-1\lt\cos\alpha\lt1$,令$t = 3-\cos\alpha\in(2,4)$,则$1-\cos^{2}\alpha=-8 + 6t - t^{2}$, 所以$\sin\theta=\frac{1}{\sqrt{10}}\cdot\sqrt{-(t+\frac{8}{t})+6}\leqslant\frac{1}{\sqrt{10}}\cdot\sqrt{-4\sqrt{2}+6}=\frac{\sqrt{10}-\sqrt{5}}{5}$, 当且仅当$t=\frac{8}{t}$,即$t = 2\sqrt{2}$,亦即$\cos\alpha=3 - 2\sqrt{2}$时,$\sin\theta$取得最大值$\frac{\sqrt{10}-\sqrt{5}}{5}$。



查看更多完整答案,请扫码查看


