2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
5. [2023·重庆永川北山中学高二月考]如图(1),在边长为 4 的菱形 ABCD 中,∠DAB = 60°,点 M,N 分别是边 BC,CD 的中点,AC∩BD = O₁,AC∩MN = G. 沿 MN 将△CMN 翻折到△PMN 的位置,连接 PA,PB,PD,得到如图(2)所示的五棱锥 P - ABMND.
(1)在翻折过程中是否总有平面 PBD⊥平面 PAC?证明你的结论.
(2)当四棱锥 P - MNDB 体积最大时,在线段 PA 上是否存在一点 Q,使平面 QMN 与平面 PMN 夹角的余弦值为$\frac{\sqrt{10}}{10}$?若存在,试确定点 Q 的位置;若不存在,请说明理由.
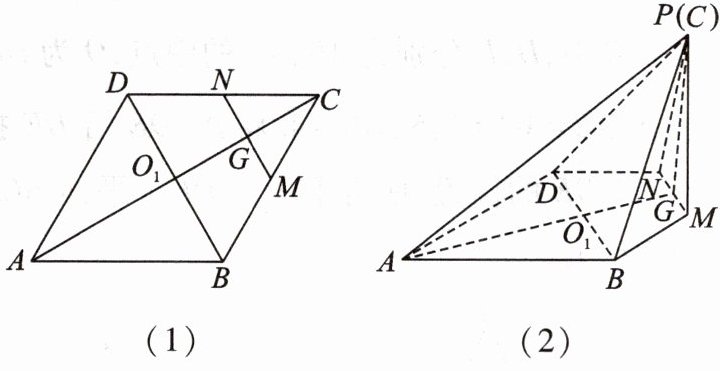
(1)在翻折过程中是否总有平面 PBD⊥平面 PAC?证明你的结论.
(2)当四棱锥 P - MNDB 体积最大时,在线段 PA 上是否存在一点 Q,使平面 QMN 与平面 PMN 夹角的余弦值为$\frac{\sqrt{10}}{10}$?若存在,试确定点 Q 的位置;若不存在,请说明理由.

答案:
【解】
(1)在翻折过程中总有平面PBD⊥平面PAG.证明如下:
∵点M,N分别是边CD,CB的中点,
∴BD∥MN. 又∠DAB = 60°,
∴易得△PMN是等边三角形. 结合题意可知G是MN的中点,
∴MN⊥PG.
∵菱形ABCD的对角线互相垂直,
∴BD⊥AC,
∴MN⊥AG.
∵AG∩PG = G,AG⊂平面PAG,PG⊂平面PAG,
∴MN⊥平面PAG,
∴BD⊥平面PAG.
∵BD⊂平面PBD,
∴平面PBD⊥平面PAG.
(2)由题意知,四边形MNDB为等腰梯形,且DB = 4,MN = 2,O₁G = $\sqrt{3}$,
∴等腰梯形MNDB的面积S = $\frac{(2 + 4)\times\sqrt{3}}{2}$ = 3$\sqrt{3}$. 要使四棱锥P - MNDB的体积最大,只要点P到平面MNDB的距离最大即可,
∴当PG⊥平面MNDB时,点P到平面MNDB的距离的最大值为PG = $\sqrt{3}$(分析出四棱锥P - MNDB体积最大成立的条件是正确求解的前提). 假设符合题意的点Q存在. 以G为原点,GA,GM,GP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系, 则A(3$\sqrt{3}$,0,0),M(0,1,0),N(0, - 1,0),P(0,0,$\sqrt{3}$),
∴$\overrightarrow{AP}$=( - 3$\sqrt{3}$,0,$\sqrt{3}$),$\overrightarrow{NM}$=(0,2,0). 由PG⊥平面MNDB,得AG⊥PG. 又AG⊥MN,且MN∩PG = G,MN⊂平面PMN,PG⊂平面PMN,
∴AG⊥平面PMN,
∴平面PMN的一个法向量n₁=(1,0,0). 设$\overrightarrow{AQ}$ = λ$\overrightarrow{AP}$(0≤λ≤1), 则$\overrightarrow{AQ}$=( - 3$\sqrt{3}$λ,0,$\sqrt{3}$λ),
∴Q(3$\sqrt{3}$(1 - λ),0,$\sqrt{3}$λ),
∴$\overrightarrow{QM}$=(3$\sqrt{3}$(λ - 1),1, - $\sqrt{3}$λ). 设平面QM的法向量为n₂=(x₂,y₂,z₂), 则$\begin{cases}n_{2}\cdot\overrightarrow{NM}=0\\n_{2}\cdot\overrightarrow{QM}=0\end{cases}$,即$\begin{cases}2y_{2}=0\\3\sqrt{3}(λ - 1)x_{2}+y_{2}- \sqrt{3}λz_{2}=0\end{cases}$. 取z₂ = 1,得y₂ = 0,x₂ = $\frac{λ}{3(λ - 1)}$,
∴n₂=($\frac{λ}{3(λ - 1)}$,0,1) = $\frac{1}{3(λ - 1)}$(λ,0,3(λ - 1)),
∴平面QM的一个法向量n=(λ,0,3(λ - 1))(用含λ的式子表示出平面QM的法向量是求解本题的关键). 设二面角Q - MN - P的平面角为θ, 则|$\cos\theta$| = $\frac{|n\cdot n_{1}|}{|n||n_{1}|}$ = $\frac{|λ|}{\sqrt{λ^{2}+9(λ - 1)^{2}}}$ = $\frac{\sqrt{10}}{10}$, 即$\frac{λ^{2}}{10λ^{2}-18λ + 9}$ = $\frac{1}{10}$,解得λ = $\frac{1}{2}$, 故符合题意的点Q存在且Q为线段PA的中点.
【解】
(1)在翻折过程中总有平面PBD⊥平面PAG.证明如下:
∵点M,N分别是边CD,CB的中点,
∴BD∥MN. 又∠DAB = 60°,
∴易得△PMN是等边三角形. 结合题意可知G是MN的中点,
∴MN⊥PG.
∵菱形ABCD的对角线互相垂直,
∴BD⊥AC,
∴MN⊥AG.
∵AG∩PG = G,AG⊂平面PAG,PG⊂平面PAG,
∴MN⊥平面PAG,
∴BD⊥平面PAG.
∵BD⊂平面PBD,
∴平面PBD⊥平面PAG.
(2)由题意知,四边形MNDB为等腰梯形,且DB = 4,MN = 2,O₁G = $\sqrt{3}$,
∴等腰梯形MNDB的面积S = $\frac{(2 + 4)\times\sqrt{3}}{2}$ = 3$\sqrt{3}$. 要使四棱锥P - MNDB的体积最大,只要点P到平面MNDB的距离最大即可,
∴当PG⊥平面MNDB时,点P到平面MNDB的距离的最大值为PG = $\sqrt{3}$(分析出四棱锥P - MNDB体积最大成立的条件是正确求解的前提). 假设符合题意的点Q存在. 以G为原点,GA,GM,GP所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系, 则A(3$\sqrt{3}$,0,0),M(0,1,0),N(0, - 1,0),P(0,0,$\sqrt{3}$),
∴$\overrightarrow{AP}$=( - 3$\sqrt{3}$,0,$\sqrt{3}$),$\overrightarrow{NM}$=(0,2,0). 由PG⊥平面MNDB,得AG⊥PG. 又AG⊥MN,且MN∩PG = G,MN⊂平面PMN,PG⊂平面PMN,
∴AG⊥平面PMN,
∴平面PMN的一个法向量n₁=(1,0,0). 设$\overrightarrow{AQ}$ = λ$\overrightarrow{AP}$(0≤λ≤1), 则$\overrightarrow{AQ}$=( - 3$\sqrt{3}$λ,0,$\sqrt{3}$λ),
∴Q(3$\sqrt{3}$(1 - λ),0,$\sqrt{3}$λ),
∴$\overrightarrow{QM}$=(3$\sqrt{3}$(λ - 1),1, - $\sqrt{3}$λ). 设平面QM的法向量为n₂=(x₂,y₂,z₂), 则$\begin{cases}n_{2}\cdot\overrightarrow{NM}=0\\n_{2}\cdot\overrightarrow{QM}=0\end{cases}$,即$\begin{cases}2y_{2}=0\\3\sqrt{3}(λ - 1)x_{2}+y_{2}- \sqrt{3}λz_{2}=0\end{cases}$. 取z₂ = 1,得y₂ = 0,x₂ = $\frac{λ}{3(λ - 1)}$,
∴n₂=($\frac{λ}{3(λ - 1)}$,0,1) = $\frac{1}{3(λ - 1)}$(λ,0,3(λ - 1)),
∴平面QM的一个法向量n=(λ,0,3(λ - 1))(用含λ的式子表示出平面QM的法向量是求解本题的关键). 设二面角Q - MN - P的平面角为θ, 则|$\cos\theta$| = $\frac{|n\cdot n_{1}|}{|n||n_{1}|}$ = $\frac{|λ|}{\sqrt{λ^{2}+9(λ - 1)^{2}}}$ = $\frac{\sqrt{10}}{10}$, 即$\frac{λ^{2}}{10λ^{2}-18λ + 9}$ = $\frac{1}{10}$,解得λ = $\frac{1}{2}$, 故符合题意的点Q存在且Q为线段PA的中点.

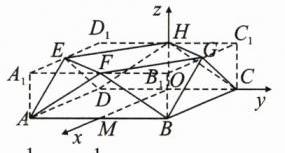
6. [2023·四川成都石室中学高三月考]已知图(1)中,A,B,C,D 是正方形 EFGH 各边的中点,分别沿着 AB,BC,CD,DA 把△ABF,△BCG,△CDH,△DAE 向上折起,使得每个三角形所在的平面都与平面 ABCD 垂直,再顺次连接 EFGH,得到一个如图(2)所示的多面体,则以下结论正确的是 (写出所有正确结论的序号).
①△AEF 是正三角形;
②平面 AEF⊥平面 CGH;
③直线 CG 与平面 AEF 所成角的正切值为$\sqrt{2}$;
④当 AB = 2 时,多面体 ABCD - EFGH 的体积为$\frac{8}{3}$.
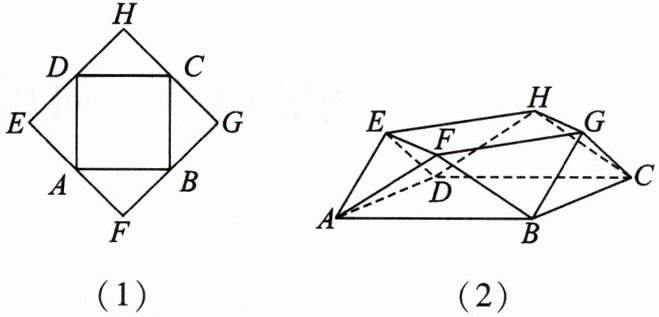
①△AEF 是正三角形;
②平面 AEF⊥平面 CGH;
③直线 CG 与平面 AEF 所成角的正切值为$\sqrt{2}$;
④当 AB = 2 时,多面体 ABCD - EFGH 的体积为$\frac{8}{3}$.

答案:
①②④
7. [2022·广东深圳外国语学校高二期末]如图(1),在矩形 ABCD 中,AB = 2AD = 2$\sqrt{2}$,E 为线段 DC 的中点,将△ADE 沿直线 AE 折起,使得 DC = $\sqrt{6}$,如图(2).
(1)求证:BE⊥平面 ADE.
(2)已知点 H 在线段 AB 上移动,设平面 ADE 与平面 DHC 所成的角为θ,求 cosθ的取值范围.
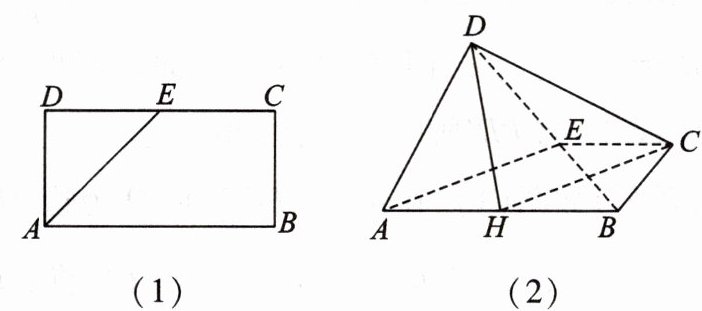
(1)求证:BE⊥平面 ADE.
(2)已知点 H 在线段 AB 上移动,设平面 ADE 与平面 DHC 所成的角为θ,求 cosθ的取值范围.

答案:
(1)【证明】取线段AE的中点O,连接DO,OC,如图. 在Rt△ADE中,DA = DE = $\sqrt{2}$,
∴DO⊥AE,AE = 2,DO = 1. 在△OEC中,OE = $\frac{1}{2}$AE = 1,EC = $\sqrt{2}$,∠OEC = $\frac{3\pi}{4}$, 由余弦定理,得OC² = 1 + 2+2×1×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$ = 5,
∴OC = $\sqrt{5}$. 在△DOC中,DC² = 6 = DO² + OC²,
∴DO⊥OC. 又AE∩OC = O,AE,OC⊂平面ABCE,
∴DO⊥平面ABCE. 又DO⊂平面ADE,
∴平面ADE⊥平面ABCE. 在△ABE中,AE = BE = 2,AB = 2$\sqrt{2}$,
∴BE⊥AE.
∵平面ADE∩平面ABCE = AE,BE⊂平面ABCE,
∴BE⊥平面ADE.
(2)【解】以E为原点,建立如图所示的空间直角坐标系, 则D(1,0,1),C( - 1,1,0),A(2,0,0),B(0,2,0). 易知平面ADE的一个法向量为n₁=(0,1,0). 设点H的坐标为(t,2 - t,0),t∈[0,2], 则$\overrightarrow{HC}$=( - t - 1,t - 1,0),$\overrightarrow{DC}$=( - 2,1, - 1). 设平面DHC的法向量为n₂=(x,y,z), 则$\begin{cases}n_{2}\cdot\overrightarrow{HC}=(-t - 1)x+(t - 1)y = 0\\n_{2}\cdot\overrightarrow{DC}=-2x + y - z = 0\end{cases}$. 令y = 1 + t,则n₂=(t - 1,1 + t,3 - t). 所以|$\cos\langle n_{1},n_{2}\rangle$| = $\frac{|n_{1}\cdot n_{2}|}{|n_{1}||n_{2}|}$ = $\frac{|1 + t|}{\sqrt{(t - 1)^{2}+(t + 1)^{2}+(3 - t)^{2}}}$. 令m = 1 + t,则m∈[1,3], 所以|$\cos\langle n_{1},n_{2}\rangle$| = $\frac{|m|}{\sqrt{(m - 2)^{2}+m^{2}+(4 - m)^{2}}}$ = $\frac{1}{\sqrt{\frac{20}{m^{2}}-\frac{12}{m}+3}}$ = $\frac{1}{\sqrt{20(\frac{1}{m}-\frac{3}{10})^{2}+\frac{6}{5}}}$. 又$\frac{1}{m}$∈[$\frac{1}{3}$,1],所以|$\cos\langle n_{1},n_{2}\rangle$|∈[$\frac{\sqrt{11}}{11}$,$\frac{3\sqrt{11}}{11}$], 所以$\cos\theta$的取值范围为[$\frac{\sqrt{11}}{11}$,$\frac{3\sqrt{11}}{11}$].

(1)【证明】取线段AE的中点O,连接DO,OC,如图. 在Rt△ADE中,DA = DE = $\sqrt{2}$,
∴DO⊥AE,AE = 2,DO = 1. 在△OEC中,OE = $\frac{1}{2}$AE = 1,EC = $\sqrt{2}$,∠OEC = $\frac{3\pi}{4}$, 由余弦定理,得OC² = 1 + 2+2×1×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$ = 5,
∴OC = $\sqrt{5}$. 在△DOC中,DC² = 6 = DO² + OC²,
∴DO⊥OC. 又AE∩OC = O,AE,OC⊂平面ABCE,
∴DO⊥平面ABCE. 又DO⊂平面ADE,
∴平面ADE⊥平面ABCE. 在△ABE中,AE = BE = 2,AB = 2$\sqrt{2}$,
∴BE⊥AE.
∵平面ADE∩平面ABCE = AE,BE⊂平面ABCE,
∴BE⊥平面ADE.
(2)【解】以E为原点,建立如图所示的空间直角坐标系, 则D(1,0,1),C( - 1,1,0),A(2,0,0),B(0,2,0). 易知平面ADE的一个法向量为n₁=(0,1,0). 设点H的坐标为(t,2 - t,0),t∈[0,2], 则$\overrightarrow{HC}$=( - t - 1,t - 1,0),$\overrightarrow{DC}$=( - 2,1, - 1). 设平面DHC的法向量为n₂=(x,y,z), 则$\begin{cases}n_{2}\cdot\overrightarrow{HC}=(-t - 1)x+(t - 1)y = 0\\n_{2}\cdot\overrightarrow{DC}=-2x + y - z = 0\end{cases}$. 令y = 1 + t,则n₂=(t - 1,1 + t,3 - t). 所以|$\cos\langle n_{1},n_{2}\rangle$| = $\frac{|n_{1}\cdot n_{2}|}{|n_{1}||n_{2}|}$ = $\frac{|1 + t|}{\sqrt{(t - 1)^{2}+(t + 1)^{2}+(3 - t)^{2}}}$. 令m = 1 + t,则m∈[1,3], 所以|$\cos\langle n_{1},n_{2}\rangle$| = $\frac{|m|}{\sqrt{(m - 2)^{2}+m^{2}+(4 - m)^{2}}}$ = $\frac{1}{\sqrt{\frac{20}{m^{2}}-\frac{12}{m}+3}}$ = $\frac{1}{\sqrt{20(\frac{1}{m}-\frac{3}{10})^{2}+\frac{6}{5}}}$. 又$\frac{1}{m}$∈[$\frac{1}{3}$,1],所以|$\cos\langle n_{1},n_{2}\rangle$|∈[$\frac{\sqrt{11}}{11}$,$\frac{3\sqrt{11}}{11}$], 所以$\cos\theta$的取值范围为[$\frac{\sqrt{11}}{11}$,$\frac{3\sqrt{11}}{11}$].

查看更多完整答案,请扫码查看


