《2025年练习生高中数学选择性必修第一册人教A版》

1. [2022·上海浦东新区高二期中]已知圆 C 的方程为$x^{2}+(y - 4)^{2}=1$，直线 l 的方程为$2x - y = 0$，点 P 在直线 l 上，过点 P 作圆 C 的切线 PA，PB，切点分别为 A，B.
(1)若∠APB = 60°，求点 P 的坐标；
(2)试证明经过 A，P，C(其中点 C 为圆 C 的圆心)三点的圆必经过定点，并求出所有定点的坐标.

答案：
(1)由已知条件可得圆 C 的圆心 C(0,4)，半径 r = 1. 在 Rt△APC 中，∠APC = \(\frac{1}{2}\times60^{\circ}=30^{\circ}\)， 所以|PC| = 2|AC| = 2. 设 P(a,2a)，则\(\sqrt{a^{2}+(2a - 4)^{2}} = 2\)，解得 a = 2 或 a = \(\frac{6}{5}\)， 所以点 P 的坐标为(2,4)或(\(\frac{6}{5}\),\(\frac{12}{5}\)).
(2)设 P(b,2b). 过点 A，P，C 的圆是以 PC 为直径的圆，其方程为 x(x - b)+(y - 4)(y - 2b)=0， 整理，得\(x^{2}+y^{2}-bx - 4y - 2by + 8b = 0\)， 即(\(x^{2}+y^{2}-4y\)) - b(x + 2y - 8)=0. 由\(\begin{cases}x^{2}+y^{2}-4y = 0 \\ x + 2y - 8 = 0 \end{cases}\)，解得\(\begin{cases}x = 0 \\ y = 4 \end{cases}\)或\(\begin{cases}x = \frac{8}{5} \\ y = \frac{16}{5} \end{cases}\)， 所以该圆必经过定点(0,4)和(\(\frac{8}{5}\),\(\frac{16}{5}\). 

2. 在平面直角坐标系中，圆 O：$x^{2}+y^{2}=16$.
(1)过点 P(4,2)作圆 O 的切线 m，求 m 的方程；
(2)直线 l：y = kx + b 与圆 O 交于 M，N 两点，已知 T(8,0)，若 x 轴平分∠MTN，试证明不论 k 取何值，直线 l 与 x 轴的交点为定点，并求出此定点坐标.

答案： 【解】
(1)当切线的斜率不存在时，切线方程为 x = 4，显然与圆 O 相切. 当切线的斜率存在时，设切线方程为 y = k(x - 4)+2， 即 kx - y - 4k + 2 = 0. 则\(\frac{|4k - 2|}{\sqrt{1 + k^{2}}}=4\)，解得 k = -\(\frac{3}{4}\)， 所以此时切线方程为 3x + 4y - 20 = 0. 综上所述，切线 m 的方程为 x = 4 或 3x + 4y - 20 = 0.
(2)设 M(\(x_{1}\),\(y_{1}\))，N(\(x_{2}\),\(y_{2}\)). 联立成方程组\(\begin{cases}y = kx + b \\ x^{2}+y^{2}=16 \end{cases}\)， 消去 y 并整理，得(1 + \(k^{2}\))\(x^{2}+2kbx + b^{2}-16 = 0\)， 则\(\Delta = 4k^{2}b^{2}-4(1 + k^{2})(b^{2}-16)>0\)，得\(b^{2}<16 + 16k^{2}\)， 所以\(x_{1}+x_{2}=\frac{-2kb}{1 + k^{2}}\)，\(x_{1}x_{2}=\frac{b^{2}-16}{1 + k^{2}}\). 因为 x 轴平分∠MTN，所以\(k_{MT}+k_{NT}=0\)， 即\(\frac{y_{1}}{x_{1}-8}+\frac{y_{2}}{x_{2}-8}=0\)， 即(\(kx_{1}+b\))(\(x_{2}-8\))+(\(kx_{2}+b\))(\(x_{1}-8\)) = 0， 所以\(2kx_{1}x_{2}+(b - 8k)(x_{1}+x_{2})-16b = 0\)， 所以\(2k(b^{2}-16)+(b - 8k)(-2kb)-16b(1 + k^{2}) = 0\)， 解得 b = -2k， 所以直线 l 的方程为 y = k(x - 2)， 所以直线 l 恒过点(2,0).

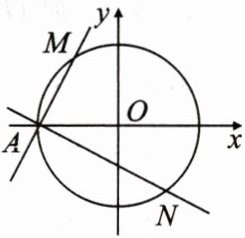
3. 如图，在平面直角坐标系中，圆 O：$x^{2}+y^{2}=4$与 x 轴负半轴交于点 A，过点 A 的直线 AM，AN 分别与圆 O 交于 M，N 两点.
(1)若$k_{AM}=2$，$k_{AN}=-\frac{1}{2}$，求△AMN 的面积；
(2)若直线 MN 过点(1,0)，试证明$k_{AM}\cdot k_{AN}$为定值，并求此定值.

答案：
(1)根据题意，圆 O:\(x^{2}+y^{2}=4\)的圆心为(0,0)，半径 r = 2，A(-2,0). 若\(k_{AM}=2\)，则直线 AM 的方程为 y - 0 = 2(x + 2)，即 y = 2x + 4. 若\(k_{AN}=-\frac{1}{2}\)，则直线 AN 的方程为 y - 0 = -\(\frac{1}{2}\)(x + 2)， 即 y = -\(\frac{1}{2}\)x - 1. 由题意，知\(k_{AM}\cdot k_{AN}=-1\)，所以 AN⊥AM， 所以 MN 为圆 O 的直径， 所以圆心到直线 AM 的距离 d = \(\frac{|4|}{\sqrt{1 + 4}}=\frac{4\sqrt{5}}{5}\)， 则|AM| = 2×\(\sqrt{r^{2}-d^{2}}=\frac{4\sqrt{5}}{5}\). 由中位线定理，知|AN| = 2d = \(\frac{8\sqrt{5}}{5}\)， 所以△AMN 的面积 S = \(\frac{1}{2}\times|AM|\times|AN|=\frac{1}{2}\times\frac{4\sqrt{5}}{5}\times\frac{8\sqrt{5}}{5}=\frac{16}{5}\).
(2)设 M(\(x_{1}\),\(y_{1}\))，N(\(x_{2}\),\(y_{2}\)). ①当直线 MN 的斜率存在时，设直线 MN 的方程为 y = k(x - 1)(k≠0)， 代入圆的方程，得\(x^{2}+k^{2}(x - 1)^{2}-4 = 0\)， 整理，得(1 + \(k^{2}\))\(x^{2}-2k^{2}x + k^{2}-4 = 0\)， 则\(x_{1}+x_{2}=\frac{2k^{2}}{1 + k^{2}}\)，\(x_{1}x_{2}=\frac{k^{2}-4}{1 + k^{2}}\)， 此时\(k_{AM}\cdot k_{AN}=\frac{y_{1}}{x_{1}+2}\cdot\frac{y_{2}}{x_{2}+2}=\frac{y_{1}y_{2}}{(x_{1}+2)(x_{2}+2)}=\frac{k^{2}(x_{1}-1)(x_{2}-1)}{(x_{1}+2)(x_{2}+2)}=k^{2}\cdot\frac{x_{1}x_{2}-(x_{1}+x_{2})+1}{x_{1}x_{2}+2(x_{1}+x_{2})+4}=-\frac{1}{3}\). ②当直线 MN 的斜率不存在时，直线 MN 的方程为 x = 1， 代入圆的方程，得 M(1,\(\sqrt{3}\))，N(1,-\(\sqrt{3}\))， 此时\(k_{AM}\cdot k_{AN}=\frac{\sqrt{3}-0}{1-(-2)}\times\frac{-\sqrt{3}-0}{1-(-2)}=-\frac{1}{3}\). 综上所述，\(k_{AM}\cdot k_{AN}\)为定值，且此定值为-\(\frac{1}{3}\).

4. 已知圆 C：$(x + 3)^{2}+(y + 4)^{2}=4$，直线 l 过定点 A(-1,0). 若 l 与圆相交于 P，Q 两点，线段 PQ 的中点为 M，又 l 与$l_{0}$：x + 2y - 2 = 0 的交点为 N，求证：|AM|·|AN|为定值.

答案： 【证明】连接 CM.
∵l 与圆相交于 P，Q 两点，
∴l 的斜率存在且不为 0. 设直线 l 的方程为 x = ty - 1. 联立成方程组\(\begin{cases}x = ty - 1 \\ x + 2y = 2 \end{cases}\)，解得\(\begin{cases}x = \frac{3t}{t + 2}-1 \\ y = \frac{3}{t + 2} \end{cases}\). 故 N(\(\frac{3t}{t + 2}-1\),\(\frac{3}{t + 2}\)).
∵线段 PQ 的中点为 M，
∴CM⊥PQ. 设直线 CM 的方程为 y + 4 = -t(x + 3). 联立成方程组\(\begin{cases}x = ty - 1 \\ y + 4 = -t(x + 3) \end{cases}\)，解得\(\begin{cases}x = \frac{-2t^{2}-4t}{t^{2}+1}-1 \\ y = \frac{-2t - 4}{t^{2}+1} \end{cases}\). 故 M(\(\frac{-2t^{2}-4t}{t^{2}+1}-1\),\(\frac{-2t - 4}{t^{2}+1}\)).
∴\(\overrightarrow{AM}=(\frac{-2t^{2}-4t}{t^{2}+1},\frac{-2t - 4}{t^{2}+1})\)，\(\overrightarrow{AN}=(\frac{3t}{t + 2},\frac{3}{t + 2})\)，
∴\(\overrightarrow{AM}\cdot\overrightarrow{AN}=-6\).
∵A，M，N 三点共线，
∴|AM|·|AN| = 6，故|AM|·|AN|为定值.