2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. [2022·山西晋中高三模拟预测]如图,点P在圆柱的上底面圆周上,四边形ABCD为圆柱下底面的内接四边形,AC为圆柱下底面的直径,PD为圆柱的母线,且PD = 3,圆柱的底面半径为1.
(1)证明:AD⊥PC.
(2)AD = $\sqrt{2}$,B为$\overset{\frown}{AC}$的中点,点Q在线段PB上,记$\overrightarrow{PQ}=2\overrightarrow{QB}$,求二面角B - AC - Q的余弦值.
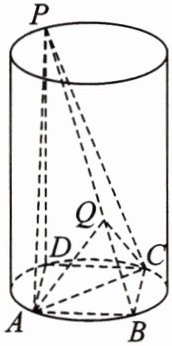
(1)证明:AD⊥PC.
(2)AD = $\sqrt{2}$,B为$\overset{\frown}{AC}$的中点,点Q在线段PB上,记$\overrightarrow{PQ}=2\overrightarrow{QB}$,求二面角B - AC - Q的余弦值.

答案:
【证明】**:因为 \(AC\) 为圆柱下底面的直径,所以 \(AD\perp DC\)。因为 \(PD\) 为圆柱的母线,所以 \(PD\perp\) 平面 \(ABCD\)。又 \(AD\subset\) 平面 \(ABCD\),所以 \(PD\perp AD\)。又 \(DC\cap PD = D\),所以 \(AD\perp\) 平面 \(PDC\)。又 \(PC\subset\) 平面 \(PDC\),所以 \(AD\perp PC\)。 - **
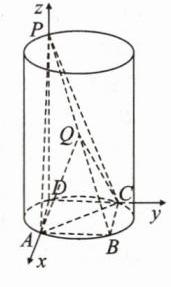
(2)【解】**:由题意可知 \(AC = 2\)。由
(1)知 \(AD\perp DC\),又 \(AD=\sqrt{2}\),所以 \(DC=\sqrt{AC^{2}-AD^{2}}=\sqrt{2}\)。又 \(B\) 为 \(\overset{\frown}{AC}\) 的中点,所以 \(AB = BC=\sqrt{2}\),即四边形 \(ABCD\) 为正方形。易知 \(DA,DC,DP\) 两两垂直,以 \(D\) 为原点,\(DA,DC,DP\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系,如图,则 \(P(0,0,3)\),\(A(\sqrt{2},0,0)\),\(B(\sqrt{2},\sqrt{2},0)\),\(C(0,\sqrt{2},0)\),所以 \(\overrightarrow{AC}=(-\sqrt{2},\sqrt{2},0)\),\(\overrightarrow{PA}=(\sqrt{2},0,-3)\),\(\overrightarrow{PB}=(\sqrt{2},\sqrt{2},-3)\)。因为 \(\overrightarrow{PQ}=2\overrightarrow{QB}\),所以 \(\overrightarrow{PQ}=\frac{2}{3}\overrightarrow{PB}=(\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3},-2)\)。所以 \(\overrightarrow{AQ}=\overrightarrow{PQ}-\overrightarrow{PA}=(-\frac{\sqrt{2}}{3},\frac{2\sqrt{2}}{3},1)\)。设平面 \(QAC\) 的法向量为 \(\boldsymbol{m}=(x,y,z)\),则 \(\begin{cases}\overrightarrow{AQ}\cdot\boldsymbol{m}=0\\\overrightarrow{AC}\cdot\boldsymbol{m}=0\end{cases}\),即 \(\begin{cases}-\frac{\sqrt{2}}{3}x+\frac{2\sqrt{2}}{3}y + z = 0\\-\sqrt{2}x+\sqrt{2}y = 0\end{cases}\)。取 \(x = 3\),则 \(y = 3\),\(z=-\sqrt{2}\),所以 \(\boldsymbol{m}=(3,3,-\sqrt{2})\)。易知平面 \(BAC\) 的一个法向量为 \(\boldsymbol{n}=(0,0,-1)\),所以 \(\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{\vert\boldsymbol{m}\vert\vert\boldsymbol{n}\vert}=\frac{\sqrt{2}}{\sqrt{9 + 9+2\times1}}=\frac{\sqrt{2}}{2\sqrt{5}}=\frac{\sqrt{10}}{10}\)。由图可知二面角 \(B - AC - Q\) 为锐二面角,所以二面角 \(B - AC - Q\) 的余弦值为 \(\frac{\sqrt{10}}{10}\)。 - **水平诊断**:此题第
(1)问用于检测知识与技能,知道线面垂直的判定定理与性质定理是知识,能够证出 \(AD\perp\) 平面 \(PDC\) 是技能。第
(2)问建立方程组求出平面 \(QAC\) 的法向量 \(\boldsymbol{m}\),进而计算两平面的法向量的夹角的余弦值,用于检测数学思想——方程思想;同时,第
(2)问中将二面角的平面角的求解转化为求平面 \(QAC\) 和平面 \(BAC\) 的法向量的夹角问题,用于检测数学思想——转化思想。其中,根据已知条件建立适当的空间直角坐标系,并求出各点的坐标,用于检测基本活动经验。

【证明】**:因为 \(AC\) 为圆柱下底面的直径,所以 \(AD\perp DC\)。因为 \(PD\) 为圆柱的母线,所以 \(PD\perp\) 平面 \(ABCD\)。又 \(AD\subset\) 平面 \(ABCD\),所以 \(PD\perp AD\)。又 \(DC\cap PD = D\),所以 \(AD\perp\) 平面 \(PDC\)。又 \(PC\subset\) 平面 \(PDC\),所以 \(AD\perp PC\)。 - **
(2)【解】**:由题意可知 \(AC = 2\)。由
(1)知 \(AD\perp DC\),又 \(AD=\sqrt{2}\),所以 \(DC=\sqrt{AC^{2}-AD^{2}}=\sqrt{2}\)。又 \(B\) 为 \(\overset{\frown}{AC}\) 的中点,所以 \(AB = BC=\sqrt{2}\),即四边形 \(ABCD\) 为正方形。易知 \(DA,DC,DP\) 两两垂直,以 \(D\) 为原点,\(DA,DC,DP\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系,如图,则 \(P(0,0,3)\),\(A(\sqrt{2},0,0)\),\(B(\sqrt{2},\sqrt{2},0)\),\(C(0,\sqrt{2},0)\),所以 \(\overrightarrow{AC}=(-\sqrt{2},\sqrt{2},0)\),\(\overrightarrow{PA}=(\sqrt{2},0,-3)\),\(\overrightarrow{PB}=(\sqrt{2},\sqrt{2},-3)\)。因为 \(\overrightarrow{PQ}=2\overrightarrow{QB}\),所以 \(\overrightarrow{PQ}=\frac{2}{3}\overrightarrow{PB}=(\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3},-2)\)。所以 \(\overrightarrow{AQ}=\overrightarrow{PQ}-\overrightarrow{PA}=(-\frac{\sqrt{2}}{3},\frac{2\sqrt{2}}{3},1)\)。设平面 \(QAC\) 的法向量为 \(\boldsymbol{m}=(x,y,z)\),则 \(\begin{cases}\overrightarrow{AQ}\cdot\boldsymbol{m}=0\\\overrightarrow{AC}\cdot\boldsymbol{m}=0\end{cases}\),即 \(\begin{cases}-\frac{\sqrt{2}}{3}x+\frac{2\sqrt{2}}{3}y + z = 0\\-\sqrt{2}x+\sqrt{2}y = 0\end{cases}\)。取 \(x = 3\),则 \(y = 3\),\(z=-\sqrt{2}\),所以 \(\boldsymbol{m}=(3,3,-\sqrt{2})\)。易知平面 \(BAC\) 的一个法向量为 \(\boldsymbol{n}=(0,0,-1)\),所以 \(\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{\vert\boldsymbol{m}\vert\vert\boldsymbol{n}\vert}=\frac{\sqrt{2}}{\sqrt{9 + 9+2\times1}}=\frac{\sqrt{2}}{2\sqrt{5}}=\frac{\sqrt{10}}{10}\)。由图可知二面角 \(B - AC - Q\) 为锐二面角,所以二面角 \(B - AC - Q\) 的余弦值为 \(\frac{\sqrt{10}}{10}\)。 - **水平诊断**:此题第
(1)问用于检测知识与技能,知道线面垂直的判定定理与性质定理是知识,能够证出 \(AD\perp\) 平面 \(PDC\) 是技能。第
(2)问建立方程组求出平面 \(QAC\) 的法向量 \(\boldsymbol{m}\),进而计算两平面的法向量的夹角的余弦值,用于检测数学思想——方程思想;同时,第
(2)问中将二面角的平面角的求解转化为求平面 \(QAC\) 和平面 \(BAC\) 的法向量的夹角问题,用于检测数学思想——转化思想。其中,根据已知条件建立适当的空间直角坐标系,并求出各点的坐标,用于检测基本活动经验。
2. [2022·广东广州高二期中]如图,在四棱锥P - ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA = $2\sqrt{3}$,G为CD的中点,E,F是棱PD上两点(F在E的上方),且EF = 2.
(1)若BF//平面AEG,求DE;
(2)当点F到平面AEC的距离取得最大值时,求直线AG与平面AEC所成角的正弦值.
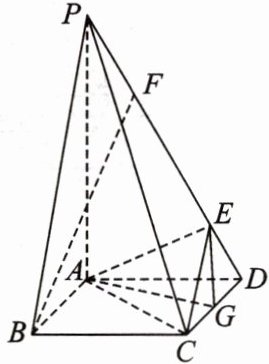
(1)若BF//平面AEG,求DE;
(2)当点F到平面AEC的距离取得最大值时,求直线AG与平面AEC所成角的正弦值.

答案:
**【解】
(1)**:连接 \(BD\),交 \(AG\) 于点 \(H\),连接 \(HE\),如图。因为 \(G\) 为 \(CD\) 的中点,所以 \(GD\parallel AB\),\(GD=\frac{1}{2}AB\),所以 \(\frac{DH}{HB}=\frac{1}{2}\)。因为 \(BF\parallel\) 平面 \(AEG\),平面 \(AEG\cap\) 平面 \(BDF = HE\),\(BF\subset\) 平面 \(BDF\),所以 \(BF\parallel HE\)。所以 \(\frac{DE}{EF}=\frac{DH}{HB}=\frac{1}{2}\)。又 \(EF = 2\),所以 \(DE = 1\)。 - **
(2)**:因为 \(PA\perp\) 平面 \(ABCD\),\(AB,AD\subset\) 平面 \(ABCD\),所以 \(PA\perp AB\),\(PA\perp AD\)。又底面 \(ABCD\) 为正方形,所以 \(AB\perp AD\)。以 \(A\) 为原点,以 \(AB,AD,AP\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系,如图,则 \(A(0,0,0)\),\(C(2,2,0)\),\(G(1,2,0)\)。因为 \(EF = 2\),点 \(C\) 到直线 \(PD\) 的距离不变,所以 \(\triangle EFC\) 的面积为定值。又点 \(A\) 到平面 \(EFC\) 的距离为定值,所以三棱锥 \(A - EFC\) 的体积为定值,即三棱锥 \(F - AEC\) 的体积为定值。所以当 \(\triangle AEC\) 的面积最小时,点 \(F\) 到平面 \(AEC\) 的距离最大。即当点 \(E\) 到直线 \(AC\) 的距离最小时,点 \(F\) 到平面 \(AEC\) 的距离最大。设 \(E(0,2 - t,\sqrt{3}t)(0\leqslant t\leqslant2)\),则 \(\overrightarrow{AE}=(0,2 - t,\sqrt{3}t)\),\(\overrightarrow{AC}=(2,2,0)\),所以点 \(E\) 到直线 \(AC\) 的距离 \(d=\sqrt{\vert\overrightarrow{AE}\vert^{2}-\frac{\vert\overrightarrow{AE}\cdot\overrightarrow{AC}\vert^{2}}{\vert\overrightarrow{AC}\vert^{2}}}=\sqrt{(2 - t)^{2}+3t^{2}-\frac{\vert2(2 - t)\vert^{2}}{2\sqrt{2}}}=\sqrt{\frac{7}{2}t^{2}-2t + 2}\)。所以当 \(t=\frac{2}{7}\) 时,点 \(E\) 到直线 \(AC\) 的距离最小,点 \(F\) 到平面 \(AEC\) 的距离最大,此时 \(\overrightarrow{AE}=(0,\frac{12}{7},\frac{2\sqrt{3}}{7})\)。设平面 \(AEC\) 的法向量为 \(\boldsymbol{m}=(x,y,z)\),则 \(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AE}=\frac{12}{7}y+\frac{2\sqrt{3}}{7}z = 0\\\boldsymbol{m}\cdot\overrightarrow{AC}=2x + 2y = 0\end{cases}\)。取 \(y=-1\),可得 \(\boldsymbol{m}=(1,-1,2\sqrt{3})\)。易知 \(\overrightarrow{AG}=(1,2,0)\)。设直线 \(AG\) 与平面 \(AEC\) 所成的角为 \(\theta\),则 \(\sin\theta=\vert\cos\langle\boldsymbol{m},\overrightarrow{AG}\rangle\vert=\frac{\vert\boldsymbol{m}\cdot\overrightarrow{AG}\vert}{\vert\boldsymbol{m}\vert\vert\overrightarrow{AG}\vert}=\frac{1}{\sqrt{14}\times\sqrt{5}}=\frac{\sqrt{70}}{70}\)。所以直线 \(AG\) 与平面 \(AEC\) 所成角的正弦值为 \(\frac{\sqrt{70}}{70}\)。 - **水平诊断**:此题第
(1)问用于检测知识与技能,知道线面平行的性质定理是知识,能够利用 \(BF\parallel\) 平面 \(AEG\) 求出 \(DE\) 是技能。第
(2)问将点到平面的距离最大值的求解问题,通过立体几何图形的体积计算,转化成点到直线的距离最小值的求解,用于检测数学思想——转化思想。其中,根据已知条件建立适当的空间直角坐标系,并求出各点的坐标,用于检测基本活动经验。
(1)**:连接 \(BD\),交 \(AG\) 于点 \(H\),连接 \(HE\),如图。因为 \(G\) 为 \(CD\) 的中点,所以 \(GD\parallel AB\),\(GD=\frac{1}{2}AB\),所以 \(\frac{DH}{HB}=\frac{1}{2}\)。因为 \(BF\parallel\) 平面 \(AEG\),平面 \(AEG\cap\) 平面 \(BDF = HE\),\(BF\subset\) 平面 \(BDF\),所以 \(BF\parallel HE\)。所以 \(\frac{DE}{EF}=\frac{DH}{HB}=\frac{1}{2}\)。又 \(EF = 2\),所以 \(DE = 1\)。 - **
(2)**:因为 \(PA\perp\) 平面 \(ABCD\),\(AB,AD\subset\) 平面 \(ABCD\),所以 \(PA\perp AB\),\(PA\perp AD\)。又底面 \(ABCD\) 为正方形,所以 \(AB\perp AD\)。以 \(A\) 为原点,以 \(AB,AD,AP\) 所在直线分别为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系,如图,则 \(A(0,0,0)\),\(C(2,2,0)\),\(G(1,2,0)\)。因为 \(EF = 2\),点 \(C\) 到直线 \(PD\) 的距离不变,所以 \(\triangle EFC\) 的面积为定值。又点 \(A\) 到平面 \(EFC\) 的距离为定值,所以三棱锥 \(A - EFC\) 的体积为定值,即三棱锥 \(F - AEC\) 的体积为定值。所以当 \(\triangle AEC\) 的面积最小时,点 \(F\) 到平面 \(AEC\) 的距离最大。即当点 \(E\) 到直线 \(AC\) 的距离最小时,点 \(F\) 到平面 \(AEC\) 的距离最大。设 \(E(0,2 - t,\sqrt{3}t)(0\leqslant t\leqslant2)\),则 \(\overrightarrow{AE}=(0,2 - t,\sqrt{3}t)\),\(\overrightarrow{AC}=(2,2,0)\),所以点 \(E\) 到直线 \(AC\) 的距离 \(d=\sqrt{\vert\overrightarrow{AE}\vert^{2}-\frac{\vert\overrightarrow{AE}\cdot\overrightarrow{AC}\vert^{2}}{\vert\overrightarrow{AC}\vert^{2}}}=\sqrt{(2 - t)^{2}+3t^{2}-\frac{\vert2(2 - t)\vert^{2}}{2\sqrt{2}}}=\sqrt{\frac{7}{2}t^{2}-2t + 2}\)。所以当 \(t=\frac{2}{7}\) 时,点 \(E\) 到直线 \(AC\) 的距离最小,点 \(F\) 到平面 \(AEC\) 的距离最大,此时 \(\overrightarrow{AE}=(0,\frac{12}{7},\frac{2\sqrt{3}}{7})\)。设平面 \(AEC\) 的法向量为 \(\boldsymbol{m}=(x,y,z)\),则 \(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AE}=\frac{12}{7}y+\frac{2\sqrt{3}}{7}z = 0\\\boldsymbol{m}\cdot\overrightarrow{AC}=2x + 2y = 0\end{cases}\)。取 \(y=-1\),可得 \(\boldsymbol{m}=(1,-1,2\sqrt{3})\)。易知 \(\overrightarrow{AG}=(1,2,0)\)。设直线 \(AG\) 与平面 \(AEC\) 所成的角为 \(\theta\),则 \(\sin\theta=\vert\cos\langle\boldsymbol{m},\overrightarrow{AG}\rangle\vert=\frac{\vert\boldsymbol{m}\cdot\overrightarrow{AG}\vert}{\vert\boldsymbol{m}\vert\vert\overrightarrow{AG}\vert}=\frac{1}{\sqrt{14}\times\sqrt{5}}=\frac{\sqrt{70}}{70}\)。所以直线 \(AG\) 与平面 \(AEC\) 所成角的正弦值为 \(\frac{\sqrt{70}}{70}\)。 - **水平诊断**:此题第
(1)问用于检测知识与技能,知道线面平行的性质定理是知识,能够利用 \(BF\parallel\) 平面 \(AEG\) 求出 \(DE\) 是技能。第
(2)问将点到平面的距离最大值的求解问题,通过立体几何图形的体积计算,转化成点到直线的距离最小值的求解,用于检测数学思想——转化思想。其中,根据已知条件建立适当的空间直角坐标系,并求出各点的坐标,用于检测基本活动经验。
查看更多完整答案,请扫码查看


