《2025年练习生高中数学选择性必修第一册人教A版》

1. 已知$A(3,6)$,$B(2,4)$,则$A$,$B$两点间的距离为 ( )
A. 5
B. $\sqrt{5}$
C. 3
D. $\sqrt{29}$

答案： B

2. (多选)直线$x + y - 1 = 0$上与点$P(-2,3)$的距离等于$\sqrt{2}$的点的坐标是 ( )
A. $(-4,5)$
B. $(-3,4)$
C. $(-1,2)$
D. $(0,1)$

答案： BC

3. 已知点$A(-\sqrt{3},0)$,$B(\cos\alpha,\sin\alpha)$且$AB = 2$,则$\alpha$的一个值为________(写出符合题意的一个答案即可).

答案： $\frac{\pi}{6}$

4. 已知等腰直角三角形$ABC$的直角顶点为$C(3,3)$,点$A$的坐标为$(0,4)$,则点$B$的坐标为________.

答案： $(4,0)$或$(2,6)$

5. [2022·安徽合肥六中高二月考]设$a,b\in\mathbf{R}$,$\sqrt{(a - 1)^2+(b - 1)^2}+\sqrt{(a + 1)^2+(b + 1)^2}$的最小值为________.

答案： $2\sqrt{2}$

6. 已知$\triangle ABC$三顶点坐标$A(-3,1)$,$B(3,-3)$,$C(1,7)$,试判断$\triangle ABC$的形状.

答案： 本题可先根据两点间距离公式分别求出$\triangle ABC$三边的长度，再根据三边长度关系判断三角形的形状。\n**步骤一：计算$\vert AB\vert$，$\vert BC\vert$，$\vert AC\vert$的长度**
根据两点间距离公式：若有两点$M(x_1,y_1)$，$N(x_2,y_2)$，则$\vert MN\vert=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$。\n计算$\vert AB\vert$：
已知$A(-3,1)$，$B(3,-3)$，将其代入两点间距离公式可得：
$\vert AB\vert=\sqrt{(3-(-3))^2+((-3)-1)^2}=\sqrt{6^2+(-4)^2}=\sqrt{36 + 16}=\sqrt{52}=2\sqrt{13}$\n计算$\vert BC\vert$：
已知$B(3,-3)$，$C(1,7)$，将其代入两点间距离公式可得：
$\vert BC\vert=\sqrt{(1 - 3)^2+(7 - (-3))^2}=\sqrt{(-2)^2+10^2}=\sqrt{4 + 100}=\sqrt{104}=2\sqrt{26}$\n计算$\vert AC\vert$：
已知$A(-3,1)$，$C(1,7)$，将其代入两点间距离公式可得：
$\vert AC\vert=\sqrt{(1 - (-3))^2+(7 - 1)^2}=\sqrt{4^2+6^2}=\sqrt{16 + 36}=\sqrt{52}=2\sqrt{13}$\n**步骤二：判断$\triangle ABC$的形状**
由上述计算可知$\vert AB\vert = \vert AC\vert = 2\sqrt{13}$，所以$\triangle ABC$是等腰三角形。
又因为$\vert AB\vert^2 + \vert AC\vert^2=(2\sqrt{13})^2+(2\sqrt{13})^2=52 + 52 = 104$，$\vert BC\vert^2=(2\sqrt{26})^2 = 104$，即$\vert AB\vert^2 + \vert AC\vert^2 = \vert BC\vert^2$，满足勾股定理，所以$\triangle ABC$是直角三角形。
综上，$\triangle ABC$是等腰直角三角形。

7. 原点到直线$x + 2y - 5 = 0$的距离为 ( )
A. 1
B. $\sqrt{3}$
C. 2
D. $\sqrt{5}$

答案： D

8. 已知点$(3,m)$到直线$x+\sqrt{3}y - 4 = 0$的距离等于1,则$m$等于 ( )
A. $\sqrt{3}$
B. $-\sqrt{3}$
C. $-\frac{\sqrt{3}}{3}$
D. $\sqrt{3}$或$-\frac{\sqrt{3}}{3}$

答案： D

9. 美术绘图中常采用“三庭五眼”作图法. 三庭:将整个脸部按照发际线至眉骨,眉骨至鼻底,鼻底至下颏的范围分为上庭、中庭、下庭,各占脸长的$\frac{1}{3}$. 五眼:指脸的宽度比例,以眼形长度为单位,把脸的宽度自左至右分成第一眼、第二眼、第三眼、第四眼、第五眼五等份. 如图,假设三庭中一庭的高度为2 cm,五眼中一眼的宽度为1 cm,若图中提供的直线$AB$近似记为该人像的刘海边缘,且该人像的鼻尖位于中庭下边界和第三眼的中点,则该人像鼻尖到刘海边缘的距离约为 ( )

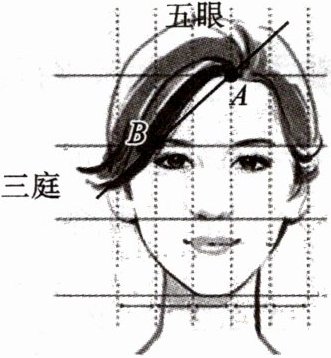
A. $\frac{5\sqrt{2}}{4}$ cm
B. $\frac{7\sqrt{2}}{4}$ cm
C. $\frac{9\sqrt{2}}{4}$ cm
D. $\frac{11\sqrt{2}}{4}$ cm

答案： 4

10. [2022·浙江杭州富阳场口中学高二期末]在平面直角坐标系$Oxy$中,$P$是曲线$y = x+\frac{4}{x}(x ＞ 0)$上的一个动点,则点$P$到直线$x + y = 0$的距离的最小值是________.

答案：
(1)
本题可先根据$B$、$C$两点坐标求出直线$BC$的斜率，再根据两直线垂直斜率之积为$-1$求出$BC$边上高所在直线的斜率，最后结合点斜式方程求出直线方程。\n**步骤一：求直线$BC$的斜率$k_{BC}$**
已知$B(4,3)$，$C(3,-2)$，根据过两点$(x_1,y_1)$，$(x_2,y_2)$直线的斜率公式$k = \frac{y_2 - y_1}{x_2 - x_1}$，可得：
$k_{BC}=\frac{3 - (-2)}{4 - 3}=\frac{5}{1}= 5$\n**步骤二：求$BC$边上高所在直线的斜率$k$**
因为$BC$边上的高与$BC$垂直，两直线垂直时斜率之积为$-1$，所以$BC$边上高所在直线的斜率$k$满足$k\cdot k_{BC} = -1$，即$k\times5 = -1$，解得$k = -\frac{1}{5}$。\n**步骤三：求$BC$边上高所在直线的方程**
已知$BC$边上的高过点$A(2,-1)$，且斜率为$-\frac{1}{5}$，根据直线的点斜式方程$y - y_0 = k(x - x_0)$（其中$(x_0,y_0)$为直线上一点，$k$为直线斜率），可得$BC$边上高所在直线的方程为：
$y - (-1)=-\frac{1}{5}(x - 2)$，即$x + 5y + 3 = 0$。
(2)
本题可先根据两点间距离公式求出$\vert BC\vert$的长度，再根据点到直线的距离公式求出点$A$到直线$BC$的距离$d$，最后根据三角形面积公式求出$\triangle ABC$的面积。\n**步骤一：求直线$BC$的方程**
已知直线$BC$过点$B(4,3)$，$C(3,-2)$，且斜率$k_{BC}= 5$，根据直线的点斜式方程可得直线$BC$的方程为：
$y - 3 = 5(x - 4)$，即$5x - y - 17 = 0$。\n**步骤二：求$\vert BC\vert$的长度**
根据两点间距离公式$\vert BC\vert=\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$，可得：
$\vert BC\vert=\sqrt{(4 - 3)^2 + (3 - (-2))^2}=\sqrt{1 + 25}=\sqrt{26}$\n**步骤三：求点$A$到直线$BC$的距离$d$**
根据点$(x_0,y_0)$到直线$Ax + By + C = 0$（$A$、$B$不同时为$0$）的距离公式$d = \frac{\vert Ax_0 + By_0 + C\vert}{\sqrt{A^2 + B^2}}$，可得点$A(2,-1)$到直线$5x - y - 17 = 0$的距离为：
$d = \frac{\vert 5\times 2 - (-1) - 17\vert}{\sqrt{5^2 + (-1)^2}}=\frac{\vert 10 + 1 - 17\vert}{\sqrt{25 + 1}}=\frac{6}{\sqrt{26}}$\n**步骤四：求$\triangle ABC$的面积$S$**
根据三角形面积公式$S = \frac{1}{2}\times底\times高$，可得：
$S_{\triangle ABC}=\frac{1}{2}\times\vert BC\vert\times d=\frac{1}{2}\times\sqrt{26}\times\frac{6}{\sqrt{26}} = 3$
综上，答案为
(1)$x + 5y + 3 = 0$；
(2)$3$。