《2025年练习生高中数学选择性必修第一册人教A版》

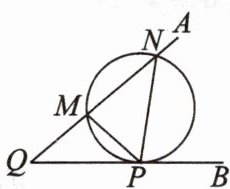
3. 几何史上有一个著名的米勒问题：“如图，设点 M，N 是锐角∠AQB 的一边 QA 上的两点，试在边 QB 上找一点 P，使得∠MPN 最大. ”其结论是：点 P 为过 M，N 两点且和射线 QB 相切的圆与射线 QB 的切点. 根据以上结论解决以下问题：在平面直角坐标系中，给定两点 M( - 1,2),N(1,4)，点 P 在 x 轴上移动，当∠MPN 取最大值时，点 P 的横坐标是 ( )

A. 1
B. - 7
C. 1 或 - 1
D. 2 或 - 7

答案： A

4. [2023·江西南昌高二联考]著名数学家欧拉提出了如下定理：三角形的外心、重心、垂心位于同一直线上，且重心到外心的距离是重心到垂心距离的一半. 此直线被称为三角形的欧拉线，该定理被称为欧拉线定理. 现已知△ABC 的三个顶点坐标分别为 A( - 1,5),B( - 3,3),C(0,2)，圆 E 的圆心 E 在△ABC 的欧拉线上，且满足 $\overrightarrow{AE}\cdot\overrightarrow{BE}=0$，直线 x + y - 6 = 0 被圆 E 截得的弦长为 2$\sqrt{3}$.
(1)求△ABC 的欧拉线的方程；
(2)求圆 E 的标准方程.

答案： 【解】
(1)由$A$，$B$，$C$的坐标，得$\triangle ABC$的重心$G(\frac{-1 - 3+0}{3},\frac{5 + 3+2}{3})$，即$G(-\frac{4}{3},\frac{10}{3})$. $\because k_{AB}=\frac{3 - 5}{-3 + 1}=1$，$k_{AC}=\frac{2 - 5}{0 + 1}=-3$， $\therefore$边$AB$的高线所在直线方程为$y=-x + 2$； 边$AC$的高线所在直线方程为$y - 3=\frac{1}{3}(x + 3)$，即$x - 3y+12 = 0$. 由$\begin{cases}y=-x + 2\\x - 3y+12 = 0\end{cases}$，得$\begin{cases}x=-\frac{3}{2}\\y=\frac{7}{2}\end{cases}$. 则$\triangle ABC$的垂心$H(-\frac{3}{2},\frac{7}{2})$. $\therefore k_{GH}=\frac{\frac{10}{3}-\frac{7}{2}}{-\frac{4}{3}+\frac{3}{2}}=-1$， 则$\triangle ABC$的欧拉线的方程为$y-\frac{7}{2}=-(x+\frac{3}{2})$，即$x + y - 2 = 0$.
(2)设$E(a,2 - a)$，圆$E$的半径为$r$， $\therefore\overrightarrow{AE}=(a + 1,-a - 3)$，$\overrightarrow{BE}=(a + 3,-a - 1)$， $\therefore\overrightarrow{AE}\cdot\overrightarrow{BE}=(a + 1)(a + 3)+(-a - 3)(-a - 1)=0$， 解得$a=-3$或$a=-1$. 当$a=-3$时，$E(-3,5)$， $\therefore$圆心$E$到直线$x + y - 6 = 0$的距离$d=\frac{4}{\sqrt{2}}=2\sqrt{2}$， $\therefore 2\sqrt{r^2 - d^2}=2\sqrt{r^2 - 8}=2\sqrt{3}$，解得$r=\sqrt{11}$. $\therefore$圆$E$的方程为$(x + 3)^2+(y - 5)^2=11$. 当$a=-1$时，$E(-1,3)$， $\therefore$圆心$E$到直线$x + y - 6 = 0$的距离$d=\frac{4}{\sqrt{2}}=2\sqrt{2}$， $\therefore 2\sqrt{r^2 - d^2}=2\sqrt{r^2 - 8}=2\sqrt{3}$，解得$r=\sqrt{11}$. $\therefore$圆$E$的方程为$(x + 1)^2+(y - 3)^2=11$. 综上所述，圆$E$的标准方程为$(x + 3)^2+(y - 5)^2=11$或$(x + 1)^2+(y - 3)^2=11$. 

5. [2022·河南焦作高二月考]已知两定点 A( - 2,0),B(1,0)，若动点 P 满足|PA| = 2|PB|，则点 P 的轨迹所包围的图形的面积等于 ( )
A. π
B. 4π
C. 8π
D. 9π

答案： B

6. 已知等腰三角形腰上的中线长为 $\sqrt{3}$，则该三角形面积的最大值为________.

答案： 2

7. [2022·湖北鄂东南高二联考]已知圆 O:x² + y² = 1 和点 A( - 2,0). 若定点 B(b,0)(b≠ - 2)和常数 λ(λ＞0)满足：对圆 O 上任意一点 M，都有|MB| = λ|MA|，则 b = ________,λ = ________.

答案： $-\frac {1}{2} \frac {1}{2}$

8. 已知在平面直角坐标系中，圆 O:x² + y² = 4，点 A( - 1,0)和点 B(0,1)，点 M 为圆 O 上的动点，则 2|MA|+|MB|的最小值为________.

答案： $\sqrt {17}$