2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
21. [2022.广东顺德一中高二月考]如图,在四棱锥$P - ABCD$中,$PA\perp$平面$ABCD$,$BC// AD$,$\angle BAD = 90^{\circ}$,$PA = AB = BC=\frac{1}{2}AD = 1$,已知$Q$是四边形$ABCD$内部一点(包括边界),且平面$QPD$与平面$APD$的夹角为$\frac{\pi}{4}$,则$\triangle ADQ$的面积的取值范围是________。


答案:
$[\frac{1}{2},1]$
22. (原创)如图,圆柱$O_{1}O_{2}$的侧面积为$2\pi$,高为 1,$AB$为$\odot O_{2}$的直径,$C$,$D$分别为$\odot O_{1}$,$\odot O_{2}$上的点,直线$CD$经过$O_{1}O_{2}$的中点$O$。
(1)若$AC = BC$,证明:$AB\perp CD$。
(2)若直线$CD$与平面$ABC$所成角的正弦值为$\frac{\sqrt{105}}{35}$,求三棱锥$D - ABC$的体积。
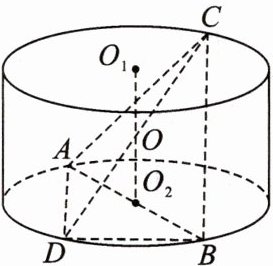
(1)若$AC = BC$,证明:$AB\perp CD$。
(2)若直线$CD$与平面$ABC$所成角的正弦值为$\frac{\sqrt{105}}{35}$,求三棱锥$D - ABC$的体积。

答案:
(1)证明:因为$AC = BC$,$O_{2}$为$AB$的中点,所以$CO_{2}\perp AB$。
又因为圆柱$O_{1}O_{2}$中,$OO_{2}\perp$平面$ABC$,$AB\subset$平面$ABC$,所以$OO_{2}\perp AB$。
因为$CO_{2}\cap OO_{2}=O_{2}$,$CO_{2}$,$OO_{2}\subset$平面$COO_{2}$,所以$AB\perp$平面$COO_{2}$。
因为$CD\subset$平面$COO_{2}$,所以$AB\perp CD$。
(2)设圆柱底面半径为$r$,由圆柱侧面积为$2\pi$,高为 1,可得$2\pi r\times1 = 2\pi$,解得$r = 1$。
以$O_{2}$为原点,分别以$O_{2}A$,$O_{2}O_{1}$所在直线为$x$,$z$轴,过$O_{2}$作垂直于$AB$的直线为$y$轴,建立空间直角坐标系。
则$A(1,0,0)$,$B(-1,0,0)$,$C(x_{0},y_{0},1)$,$D(-x_{0},-y_{0},0)$,$O(0,0,\frac{1}{2})$,$\overrightarrow{CD}=(-2x_{0},-2y_{0},-1)$。
设平面$ABC$的法向量为$\boldsymbol{n}=(x,y,z)$,$\overrightarrow{AB}=(-2,0,0)$,$\overrightarrow{AC}=(x_{0}-1,y_{0},1)$。
由$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=-2x = 0\\\boldsymbol{n}\cdot\overrightarrow{AC}=(x_{0}-1)x + y_{0}y+z = 0\end{cases}$,取$y = 1$,则$z=-y_{0}$,所以$\boldsymbol{n}=(0,1,-y_{0})$。
因为直线$CD$与平面$ABC$所成角的正弦值为$\frac{\sqrt{105}}{35}$,所以$\vert\cos\langle\overrightarrow{CD},\boldsymbol{n}\rangle\vert=\frac{\vert\overrightarrow{CD}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{CD}\vert\vert\boldsymbol{n}\vert}=\frac{\vert - 2y_{0}+y_{0}\vert}{\sqrt{4x_{0}^{2}+4y_{0}^{2}+1}\cdot\sqrt{1 + y_{0}^{2}}}=\frac{\sqrt{105}}{35}$。
又$x_{0}^{2}+y_{0}^{2}=1$,联立解得$y_{0}=\pm\frac{\sqrt{3}}{2}$。
$S_{\triangle ABC}=\frac{1}{2}\times AB\times CO_{2}=\frac{1}{2}\times2\times1 = 1$,点$D$到平面$ABC$的距离$h = 1$。
所以$V_{D - ABC}=\frac{1}{3}S_{\triangle ABC}\cdot h=\frac{1}{3}\times1\times1=\frac{1}{3}$。
(1)证明:因为$AC = BC$,$O_{2}$为$AB$的中点,所以$CO_{2}\perp AB$。
又因为圆柱$O_{1}O_{2}$中,$OO_{2}\perp$平面$ABC$,$AB\subset$平面$ABC$,所以$OO_{2}\perp AB$。
因为$CO_{2}\cap OO_{2}=O_{2}$,$CO_{2}$,$OO_{2}\subset$平面$COO_{2}$,所以$AB\perp$平面$COO_{2}$。
因为$CD\subset$平面$COO_{2}$,所以$AB\perp CD$。
(2)设圆柱底面半径为$r$,由圆柱侧面积为$2\pi$,高为 1,可得$2\pi r\times1 = 2\pi$,解得$r = 1$。
以$O_{2}$为原点,分别以$O_{2}A$,$O_{2}O_{1}$所在直线为$x$,$z$轴,过$O_{2}$作垂直于$AB$的直线为$y$轴,建立空间直角坐标系。
则$A(1,0,0)$,$B(-1,0,0)$,$C(x_{0},y_{0},1)$,$D(-x_{0},-y_{0},0)$,$O(0,0,\frac{1}{2})$,$\overrightarrow{CD}=(-2x_{0},-2y_{0},-1)$。
设平面$ABC$的法向量为$\boldsymbol{n}=(x,y,z)$,$\overrightarrow{AB}=(-2,0,0)$,$\overrightarrow{AC}=(x_{0}-1,y_{0},1)$。
由$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AB}=-2x = 0\\\boldsymbol{n}\cdot\overrightarrow{AC}=(x_{0}-1)x + y_{0}y+z = 0\end{cases}$,取$y = 1$,则$z=-y_{0}$,所以$\boldsymbol{n}=(0,1,-y_{0})$。
因为直线$CD$与平面$ABC$所成角的正弦值为$\frac{\sqrt{105}}{35}$,所以$\vert\cos\langle\overrightarrow{CD},\boldsymbol{n}\rangle\vert=\frac{\vert\overrightarrow{CD}\cdot\boldsymbol{n}\vert}{\vert\overrightarrow{CD}\vert\vert\boldsymbol{n}\vert}=\frac{\vert - 2y_{0}+y_{0}\vert}{\sqrt{4x_{0}^{2}+4y_{0}^{2}+1}\cdot\sqrt{1 + y_{0}^{2}}}=\frac{\sqrt{105}}{35}$。
又$x_{0}^{2}+y_{0}^{2}=1$,联立解得$y_{0}=\pm\frac{\sqrt{3}}{2}$。
$S_{\triangle ABC}=\frac{1}{2}\times AB\times CO_{2}=\frac{1}{2}\times2\times1 = 1$,点$D$到平面$ABC$的距离$h = 1$。
所以$V_{D - ABC}=\frac{1}{3}S_{\triangle ABC}\cdot h=\frac{1}{3}\times1\times1=\frac{1}{3}$。
23. [2022.江西景德镇一中高二期末]如图,正三棱柱$ABC - A_{1}B_{1}C_{1}$的所有棱长均为 2,$D$为棱$BB_{1}$(不包括端点)上一动点,$E$是$AB$的中点。
(1)若$AD\perp A_{1}C$,求$BD$的长;
(2)当$D$在棱$BB_{1}$(不包括端点)上运动时,求平面$ADC_{1}$与平面$ABC$的夹角的余弦值的最大值。

(1)若$AD\perp A_{1}C$,求$BD$的长;
(2)当$D$在棱$BB_{1}$(不包括端点)上运动时,求平面$ADC_{1}$与平面$ABC$的夹角的余弦值的最大值。

答案:
(1)以$E$为原点,$EA$,$EC$,$EE_{1}$($E_{1}$为$A_{1}B_{1}$中点)所在直线分别为$x$,$y$,$z$轴,建立空间直角坐标系。
则$A(1,0,0)$,$C(0,\sqrt{3},0)$,$A_{1}(1,0,2)$,设$D( - 1,0,z)$,$0\lt z\lt2$。
$\overrightarrow{AD}=(-2,0,z)$,$\overrightarrow{A_{1}C}=(-1,\sqrt{3}, - 2)$。
因为$AD\perp A_{1}C$,所以$\overrightarrow{AD}\cdot\overrightarrow{A_{1}C}=(-2)\times(-1)+0\times\sqrt{3}+z\times(-2)=0$,解得$z = 1$,即$BD = 1$。
(2)由
(1)知$A(1,0,0)$,$C_{1}(0,\sqrt{3},2)$,$D(-1,0,z)$,$0\lt z\lt2$。
$\overrightarrow{AD}=(-2,0,z)$,$\overrightarrow{AC_{1}}=(-1,\sqrt{3},2)$。
设平面$ADC_{1}$的法向量为$\boldsymbol{n}=(x,y,z_{1})$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AD}=-2x + z_{1}z = 0\\\boldsymbol{n}\cdot\overrightarrow{AC_{1}}=-x+\sqrt{3}y + 2z_{1}= 0\end{cases}$。
令$z_{1}=2$,则$x = z$,$y=\frac{z - 4}{2\sqrt{3}}$,所以$\boldsymbol{n}=(z,\frac{z - 4}{2\sqrt{3}},2)$。
平面$ABC$的一个法向量为$\boldsymbol{m}=(0,0,1)$。
设平面$ADC_{1}$与平面$ABC$的夹角为$\theta$,则$\cos\theta=\vert\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle\vert=\frac{\vert\boldsymbol{n}\cdot\boldsymbol{m}\vert}{\vert\boldsymbol{n}\vert\vert\boldsymbol{m}\vert}=\frac{2}{\sqrt{z^{2}+\frac{(z - 4)^{2}}{12}+4}}$。
令$t = z^{2}+\frac{(z - 4)^{2}}{12}+4=\frac{12z^{2}+z^{2}-8z + 16 + 48}{12}=\frac{13z^{2}-8z + 64}{12}$,其对称轴为$z=\frac{4}{13}$。
因为$0\lt z\lt2$,当$z=\frac{4}{13}$时,$t$取得最小值,此时$\cos\theta$取得最大值为$\frac{2\sqrt{13}}{13}$。
(1)以$E$为原点,$EA$,$EC$,$EE_{1}$($E_{1}$为$A_{1}B_{1}$中点)所在直线分别为$x$,$y$,$z$轴,建立空间直角坐标系。
则$A(1,0,0)$,$C(0,\sqrt{3},0)$,$A_{1}(1,0,2)$,设$D( - 1,0,z)$,$0\lt z\lt2$。
$\overrightarrow{AD}=(-2,0,z)$,$\overrightarrow{A_{1}C}=(-1,\sqrt{3}, - 2)$。
因为$AD\perp A_{1}C$,所以$\overrightarrow{AD}\cdot\overrightarrow{A_{1}C}=(-2)\times(-1)+0\times\sqrt{3}+z\times(-2)=0$,解得$z = 1$,即$BD = 1$。
(2)由
(1)知$A(1,0,0)$,$C_{1}(0,\sqrt{3},2)$,$D(-1,0,z)$,$0\lt z\lt2$。
$\overrightarrow{AD}=(-2,0,z)$,$\overrightarrow{AC_{1}}=(-1,\sqrt{3},2)$。
设平面$ADC_{1}$的法向量为$\boldsymbol{n}=(x,y,z_{1})$,则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AD}=-2x + z_{1}z = 0\\\boldsymbol{n}\cdot\overrightarrow{AC_{1}}=-x+\sqrt{3}y + 2z_{1}= 0\end{cases}$。
令$z_{1}=2$,则$x = z$,$y=\frac{z - 4}{2\sqrt{3}}$,所以$\boldsymbol{n}=(z,\frac{z - 4}{2\sqrt{3}},2)$。
平面$ABC$的一个法向量为$\boldsymbol{m}=(0,0,1)$。
设平面$ADC_{1}$与平面$ABC$的夹角为$\theta$,则$\cos\theta=\vert\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle\vert=\frac{\vert\boldsymbol{n}\cdot\boldsymbol{m}\vert}{\vert\boldsymbol{n}\vert\vert\boldsymbol{m}\vert}=\frac{2}{\sqrt{z^{2}+\frac{(z - 4)^{2}}{12}+4}}$。
令$t = z^{2}+\frac{(z - 4)^{2}}{12}+4=\frac{12z^{2}+z^{2}-8z + 16 + 48}{12}=\frac{13z^{2}-8z + 64}{12}$,其对称轴为$z=\frac{4}{13}$。
因为$0\lt z\lt2$,当$z=\frac{4}{13}$时,$t$取得最小值,此时$\cos\theta$取得最大值为$\frac{2\sqrt{13}}{13}$。
24. [2023.湖南长沙一中高三月考]如图,在直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$AB = BB_{1} = 2$,$BC\perp BA_{1}$。
(1)求证:$BC\perp AB$。
(2)若$E$为$A_{1}B$的中点,三棱锥$A - CEA_{1}$的体积为$\frac{1}{3}$,线段$CE$上是否存在点$P$,使得二面角$P - AB - E$的大小为$30^{\circ}$?若存在,求$\frac{EP}{EC}$的值;若不存在,请说明理由。
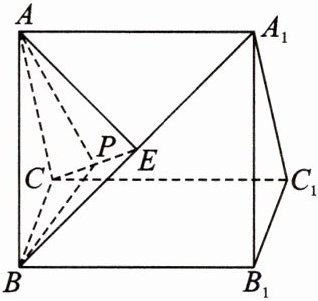
(1)求证:$BC\perp AB$。
(2)若$E$为$A_{1}B$的中点,三棱锥$A - CEA_{1}$的体积为$\frac{1}{3}$,线段$CE$上是否存在点$P$,使得二面角$P - AB - E$的大小为$30^{\circ}$?若存在,求$\frac{EP}{EC}$的值;若不存在,请说明理由。

答案:
(1)证明:因为直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$AA_{1}\perp$平面$ABC$,$BC\subset$平面$ABC$,所以$AA_{1}\perp BC$。
又因为$BC\perp BA_{1}$,$AA_{1}\cap BA_{1}=A_{1}$,$AA_{1}$,$BA_{1}\subset$平面$AA_{1}B_{1}B$,所以$BC\perp$平面$AA_{1}B_{1}B$。
因为$AB\subset$平面$AA_{1}B_{1}B$,所以$BC\perp AB$。
(2)以$B$为原点,$BA$,$BC$,$BB_{1}$所在直线分别为$x$,$y$,$z$轴,建立空间直角坐标系。
设$BC = a$,则$A(2,0,0)$,$C(0,a,0)$,$A_{1}(2,0,2)$,$E(1,0,1)$。
$V_{A - CEA_{1}}=V_{C - AA_{1}E}=\frac{1}{3}S_{\triangle AA_{1}E}\cdot BC$,$S_{\triangle AA_{1}E}=\frac{1}{2}\times2\times1 = 1$。
由$V_{A - CEA_{1}}=\frac{1}{3}$,可得$\frac{1}{3}\times1\times a=\frac{1}{3}$,解得$a = 1$。
所以$C(0,1,0)$,$\overrightarrow{CE}=(1, - 1,1)$,设$\overrightarrow{EP}=\lambda\overrightarrow{EC}$,$0\leqslant\lambda\leqslant1$,则$\overrightarrow{BP}=\overrightarrow{BE}+\overrightarrow{EP}=(1,0,1)+\lambda(-1,1, - 1)=(1 - \lambda,\lambda,1 - \lambda)$。
平面$ABE$的一个法向量为$\boldsymbol{n}_{1}=(0,1,0)$。
设平面$ABP$的法向量为$\boldsymbol{n}_{2}=(x,y,z)$,$\overrightarrow{AB}=(-2,0,0)$,$\overrightarrow{BP}=(1 - \lambda,\lambda,1 - \lambda)$。
由$\begin{cases}\boldsymbol{n}_{2}\cdot\overrightarrow{AB}=-2x = 0\\\boldsymbol{n}_{2}\cdot\overrightarrow{BP}=(1 - \lambda)x+\lambda y+(1 - \lambda)z = 0\end{cases}$,取$y = \lambda - 1$,则$z=\lambda$,所以$\boldsymbol{n}_{2}=(0,\lambda - 1,\lambda)$。
因为二面角$P - AB - E$的大小为$30^{\circ}$,所以$\vert\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle\vert=\frac{\vert\boldsymbol{n}_{1}\cdot\boldsymbol{n}_{2}\vert}{\vert\boldsymbol{n}_{1}\vert\vert\boldsymbol{n}_{2}\vert}=\frac{\vert\lambda - 1\vert}{\sqrt{(\lambda - 1)^{2}+\lambda^{2}}}=\frac{\sqrt{3}}{2}$。
整理得$4(\lambda - 1)^{2}=3((\lambda - 1)^{2}+\lambda^{2})$,即$(\lambda - 1)^{2}=3\lambda^{2}$,$2\lambda^{2}+2\lambda - 1 = 0$。
解得$\lambda=\frac{-1\pm\sqrt{3}}{2}$,因为$0\leqslant\lambda\leqslant1$,所以$\lambda=\frac{\sqrt{3}-1}{2}$,即$\frac{EP}{EC}=\frac{\sqrt{3}-1}{2}$。所以线段$CE$上存在点$P$,使得二面角$P - AB - E$的大小为$30^{\circ}$,且$\frac{EP}{EC}=\frac{\sqrt{3}-1}{2}$。
(1)证明:因为直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$AA_{1}\perp$平面$ABC$,$BC\subset$平面$ABC$,所以$AA_{1}\perp BC$。
又因为$BC\perp BA_{1}$,$AA_{1}\cap BA_{1}=A_{1}$,$AA_{1}$,$BA_{1}\subset$平面$AA_{1}B_{1}B$,所以$BC\perp$平面$AA_{1}B_{1}B$。
因为$AB\subset$平面$AA_{1}B_{1}B$,所以$BC\perp AB$。
(2)以$B$为原点,$BA$,$BC$,$BB_{1}$所在直线分别为$x$,$y$,$z$轴,建立空间直角坐标系。
设$BC = a$,则$A(2,0,0)$,$C(0,a,0)$,$A_{1}(2,0,2)$,$E(1,0,1)$。
$V_{A - CEA_{1}}=V_{C - AA_{1}E}=\frac{1}{3}S_{\triangle AA_{1}E}\cdot BC$,$S_{\triangle AA_{1}E}=\frac{1}{2}\times2\times1 = 1$。
由$V_{A - CEA_{1}}=\frac{1}{3}$,可得$\frac{1}{3}\times1\times a=\frac{1}{3}$,解得$a = 1$。
所以$C(0,1,0)$,$\overrightarrow{CE}=(1, - 1,1)$,设$\overrightarrow{EP}=\lambda\overrightarrow{EC}$,$0\leqslant\lambda\leqslant1$,则$\overrightarrow{BP}=\overrightarrow{BE}+\overrightarrow{EP}=(1,0,1)+\lambda(-1,1, - 1)=(1 - \lambda,\lambda,1 - \lambda)$。
平面$ABE$的一个法向量为$\boldsymbol{n}_{1}=(0,1,0)$。
设平面$ABP$的法向量为$\boldsymbol{n}_{2}=(x,y,z)$,$\overrightarrow{AB}=(-2,0,0)$,$\overrightarrow{BP}=(1 - \lambda,\lambda,1 - \lambda)$。
由$\begin{cases}\boldsymbol{n}_{2}\cdot\overrightarrow{AB}=-2x = 0\\\boldsymbol{n}_{2}\cdot\overrightarrow{BP}=(1 - \lambda)x+\lambda y+(1 - \lambda)z = 0\end{cases}$,取$y = \lambda - 1$,则$z=\lambda$,所以$\boldsymbol{n}_{2}=(0,\lambda - 1,\lambda)$。
因为二面角$P - AB - E$的大小为$30^{\circ}$,所以$\vert\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle\vert=\frac{\vert\boldsymbol{n}_{1}\cdot\boldsymbol{n}_{2}\vert}{\vert\boldsymbol{n}_{1}\vert\vert\boldsymbol{n}_{2}\vert}=\frac{\vert\lambda - 1\vert}{\sqrt{(\lambda - 1)^{2}+\lambda^{2}}}=\frac{\sqrt{3}}{2}$。
整理得$4(\lambda - 1)^{2}=3((\lambda - 1)^{2}+\lambda^{2})$,即$(\lambda - 1)^{2}=3\lambda^{2}$,$2\lambda^{2}+2\lambda - 1 = 0$。
解得$\lambda=\frac{-1\pm\sqrt{3}}{2}$,因为$0\leqslant\lambda\leqslant1$,所以$\lambda=\frac{\sqrt{3}-1}{2}$,即$\frac{EP}{EC}=\frac{\sqrt{3}-1}{2}$。所以线段$CE$上存在点$P$,使得二面角$P - AB - E$的大小为$30^{\circ}$,且$\frac{EP}{EC}=\frac{\sqrt{3}-1}{2}$。
1. [2023·辽宁锦州北镇满族高级中学高二期中]如图,在四棱锥 P - ABCD 中,PA⊥平面 ABCD,AB⊥AD,AB//DC,AD = DC = AP = 2,AB = 1,点 E 为棱 PC 的中点.
(1)求直线 BE 与平面 PBD 所成角的正弦值.
(2)在棱 PC 上是否存在一点 F,满足 BF⊥AC?若存在,试确定点 F 的位置;若不存在,请说明理由.
(1)求直线 BE 与平面 PBD 所成角的正弦值.
(2)在棱 PC 上是否存在一点 F,满足 BF⊥AC?若存在,试确定点 F 的位置;若不存在,请说明理由.
答案:
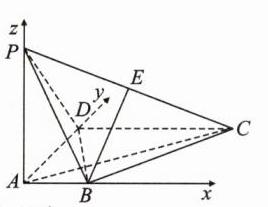
(1)由题意,易知AB,AD,AP两两垂直. 以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图, 则A(0,0,0),B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(1,1,1), 所以\(\overrightarrow{BE}=(0,1,1)\),\(\overrightarrow{PB}=(1,0, - 2)\),\(\overrightarrow{BD}=( - 1,2,0)\). 设平面PBD的法向量为\(\boldsymbol{m}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{BD}=-x + 2y = 0\\\boldsymbol{m}\cdot\overrightarrow{PB}=x - 2z = 0\end{cases}\) 取\(y = 1\),则\(\boldsymbol{m}=(2,1,1)\). 所以\(\vert\cos\langle\boldsymbol{m},\overrightarrow{BE}\rangle\vert=\frac{\vert\boldsymbol{m}\cdot\overrightarrow{BE}\vert}{\vert\boldsymbol{m}\vert\vert\overrightarrow{BE}\vert}=\frac{2}{\sqrt{6}\times\sqrt{2}}=\frac{\sqrt{3}}{3}\), 所以直线BE与平面PBD所成角的正弦值为\(\frac{\sqrt{3}}{3}\).
(2)由
(1)知\(\overrightarrow{AC}=(2,2,0)\),\(\overrightarrow{CP}=( - 2, - 2,2)\),\(\overrightarrow{BC}=(1,2,0)\). 假设存在点F,设\(\overrightarrow{CF}=\lambda\overrightarrow{CP}(0\leqslant\lambda\leqslant1)\), 则\(\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{CF}=(1 - 2\lambda,2 - 2\lambda,2\lambda)\). 由\(BF\perp AC\),得\(\overrightarrow{BF}\cdot\overrightarrow{AC}=2(1 - 2\lambda)+2(2 - 2\lambda)=0\), 解得\(\lambda=\frac{3}{4}\). 所以在棱PC上存在一点F,满足\(BF\perp AC\),此时F为PC的四等分点(靠近P点). ●方法总结 利用空间向量法解决立体几何中的探索性问题的思路:
(1)根据题设中的垂直关系,建立适当的空间直角坐标系,将相关点、相关向量用坐标表示;
(2)假设所求的点或参数存在,并用相关参数表示相关点的坐标,根据线、面满足的位置关系、数量关系,构建方程(组)求解,若能求出参数的值且符合参数的限定范围,则存在,否则不存在.

(1)由题意,易知AB,AD,AP两两垂直. 以A为原点,AB,AD,AP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图, 则A(0,0,0),B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(1,1,1), 所以\(\overrightarrow{BE}=(0,1,1)\),\(\overrightarrow{PB}=(1,0, - 2)\),\(\overrightarrow{BD}=( - 1,2,0)\). 设平面PBD的法向量为\(\boldsymbol{m}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{BD}=-x + 2y = 0\\\boldsymbol{m}\cdot\overrightarrow{PB}=x - 2z = 0\end{cases}\) 取\(y = 1\),则\(\boldsymbol{m}=(2,1,1)\). 所以\(\vert\cos\langle\boldsymbol{m},\overrightarrow{BE}\rangle\vert=\frac{\vert\boldsymbol{m}\cdot\overrightarrow{BE}\vert}{\vert\boldsymbol{m}\vert\vert\overrightarrow{BE}\vert}=\frac{2}{\sqrt{6}\times\sqrt{2}}=\frac{\sqrt{3}}{3}\), 所以直线BE与平面PBD所成角的正弦值为\(\frac{\sqrt{3}}{3}\).
(2)由
(1)知\(\overrightarrow{AC}=(2,2,0)\),\(\overrightarrow{CP}=( - 2, - 2,2)\),\(\overrightarrow{BC}=(1,2,0)\). 假设存在点F,设\(\overrightarrow{CF}=\lambda\overrightarrow{CP}(0\leqslant\lambda\leqslant1)\), 则\(\overrightarrow{BF}=\overrightarrow{BC}+\overrightarrow{CF}=(1 - 2\lambda,2 - 2\lambda,2\lambda)\). 由\(BF\perp AC\),得\(\overrightarrow{BF}\cdot\overrightarrow{AC}=2(1 - 2\lambda)+2(2 - 2\lambda)=0\), 解得\(\lambda=\frac{3}{4}\). 所以在棱PC上存在一点F,满足\(BF\perp AC\),此时F为PC的四等分点(靠近P点). ●方法总结 利用空间向量法解决立体几何中的探索性问题的思路:
(1)根据题设中的垂直关系,建立适当的空间直角坐标系,将相关点、相关向量用坐标表示;
(2)假设所求的点或参数存在,并用相关参数表示相关点的坐标,根据线、面满足的位置关系、数量关系,构建方程(组)求解,若能求出参数的值且符合参数的限定范围,则存在,否则不存在.
2. [2022·山东临沂兰陵四中高二期末]如图,四棱锥 P - ABCD 的底面 ABCD 为菱形,平面 PAD⊥平面 ABCD,∠BAD = 60°,PA = PD = √5,AB = 2,M 为 PC 上一点,且 PM = 3MC.
(1)求异面直线 AP 与 DM 所成角的余弦值.
(2)在棱 PB 上是否存在点 N,使 AN//平面 BDM?若存在,求出 PN/PB 的值;若不存在,说明理由.
(1)求异面直线 AP 与 DM 所成角的余弦值.
(2)在棱 PB 上是否存在点 N,使 AN//平面 BDM?若存在,求出 PN/PB 的值;若不存在,说明理由.
答案:

(1)取AD的中点O,连接OP,OB,如图. 因为\(PA = PD\),所以\(OP\perp AD\). 因为平面\(PAD\perp\)平面\(ABCD\)且平面\(PAD\cap\)平面\(ABCD = AD\),\(OP\subset\)平面\(PAD\), 所以\(OP\perp\)平面\(ABCD\). 因为\(OB\subset\)平面\(ABCD\),所以\(OP\perp OB\). 在菱形ABCD中,\(\angle BAD = 60^{\circ}\),所以三角形ABD是等边三角形,所以\(OB\perp AD\). 所以OA,OB,OP两两相互垂直,由此建立空间直角坐标系, 则\(P(0,0,2)\),\(A(1,0,0)\),\(B(0,\sqrt{3},0)\),\(C( - 2,\sqrt{3},0)\),\(D( - 1,0,0)\), 所以\(\overrightarrow{AP}=( - 1,0,2)\),\(\overrightarrow{DP}=(1,0,2)\),\(\overrightarrow{PC}=( - 2,\sqrt{3}, - 2)\). 所以\(\overrightarrow{DM}=\overrightarrow{DP}+\overrightarrow{PM}=\overrightarrow{DP}+\frac{3}{4}\overrightarrow{PC}=(1,0,2)+\frac{3}{4}( - 2,\sqrt{3}, - 2)=(-\frac{1}{2},\frac{3\sqrt{3}}{4},\frac{1}{2})\). 设直线AP与DM所成的角为\(\theta\), 则\(\cos\theta=\vert\frac{\overrightarrow{AP}\cdot\overrightarrow{DM}}{\vert\overrightarrow{AP}\vert\vert\overrightarrow{DM}\vert}\vert=\frac{\vert-\frac{1}{2}+1\vert}{\sqrt{5}\times\sqrt{\frac{1}{4}+\frac{27}{16}+\frac{1}{4}}}=\frac{6\sqrt{7}}{35}\).
(2)由
(1)知\(\overrightarrow{AP}=( - 1,0,2)\),\(\overrightarrow{PB}=(0,\sqrt{3}, - 2)\),\(\overrightarrow{DM}=(-\frac{1}{2},\frac{3\sqrt{3}}{4},\frac{1}{2})\),\(\overrightarrow{DB}=(1,\sqrt{3},0)\). 设平面BDM的法向量为\(\boldsymbol{n}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{DM}=-\frac{1}{2}x+\frac{3\sqrt{3}}{4}y+\frac{1}{2}z = 0\\\boldsymbol{n}\cdot\overrightarrow{DB}=x+\sqrt{3}y = 0\end{cases}\) 取\(x = - 6\),得\(\boldsymbol{n}=( - 6,2\sqrt{3}, - 15)\). 设\(\frac{PN}{PB}=\lambda\),则\(\overrightarrow{PN}=\lambda\overrightarrow{PB}(0\lt\lambda\lt1)\), 所以\(\overrightarrow{AN}=\overrightarrow{AP}+\overrightarrow{PN}=\overrightarrow{AP}+\lambda\overrightarrow{PB}=( - 1,0,2)+\lambda(0,\sqrt{3}, - 2)=( - 1,\sqrt{3}\lambda,2 - 2\lambda)\). 若\(AN\parallel\)平面\(BDM\),则\(\overrightarrow{AN}\cdot\boldsymbol{n}=6 + 6\lambda-15(2 - 2\lambda)= - 24 + 36\lambda = 0\), 解得\(\lambda=\frac{2}{3}\). 所以在棱PB上存在点N,使\(AN\parallel\)平面\(BDM\),此时\(\frac{PN}{PB}=\frac{2}{3}\).

(1)取AD的中点O,连接OP,OB,如图. 因为\(PA = PD\),所以\(OP\perp AD\). 因为平面\(PAD\perp\)平面\(ABCD\)且平面\(PAD\cap\)平面\(ABCD = AD\),\(OP\subset\)平面\(PAD\), 所以\(OP\perp\)平面\(ABCD\). 因为\(OB\subset\)平面\(ABCD\),所以\(OP\perp OB\). 在菱形ABCD中,\(\angle BAD = 60^{\circ}\),所以三角形ABD是等边三角形,所以\(OB\perp AD\). 所以OA,OB,OP两两相互垂直,由此建立空间直角坐标系, 则\(P(0,0,2)\),\(A(1,0,0)\),\(B(0,\sqrt{3},0)\),\(C( - 2,\sqrt{3},0)\),\(D( - 1,0,0)\), 所以\(\overrightarrow{AP}=( - 1,0,2)\),\(\overrightarrow{DP}=(1,0,2)\),\(\overrightarrow{PC}=( - 2,\sqrt{3}, - 2)\). 所以\(\overrightarrow{DM}=\overrightarrow{DP}+\overrightarrow{PM}=\overrightarrow{DP}+\frac{3}{4}\overrightarrow{PC}=(1,0,2)+\frac{3}{4}( - 2,\sqrt{3}, - 2)=(-\frac{1}{2},\frac{3\sqrt{3}}{4},\frac{1}{2})\). 设直线AP与DM所成的角为\(\theta\), 则\(\cos\theta=\vert\frac{\overrightarrow{AP}\cdot\overrightarrow{DM}}{\vert\overrightarrow{AP}\vert\vert\overrightarrow{DM}\vert}\vert=\frac{\vert-\frac{1}{2}+1\vert}{\sqrt{5}\times\sqrt{\frac{1}{4}+\frac{27}{16}+\frac{1}{4}}}=\frac{6\sqrt{7}}{35}\).
(2)由
(1)知\(\overrightarrow{AP}=( - 1,0,2)\),\(\overrightarrow{PB}=(0,\sqrt{3}, - 2)\),\(\overrightarrow{DM}=(-\frac{1}{2},\frac{3\sqrt{3}}{4},\frac{1}{2})\),\(\overrightarrow{DB}=(1,\sqrt{3},0)\). 设平面BDM的法向量为\(\boldsymbol{n}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{DM}=-\frac{1}{2}x+\frac{3\sqrt{3}}{4}y+\frac{1}{2}z = 0\\\boldsymbol{n}\cdot\overrightarrow{DB}=x+\sqrt{3}y = 0\end{cases}\) 取\(x = - 6\),得\(\boldsymbol{n}=( - 6,2\sqrt{3}, - 15)\). 设\(\frac{PN}{PB}=\lambda\),则\(\overrightarrow{PN}=\lambda\overrightarrow{PB}(0\lt\lambda\lt1)\), 所以\(\overrightarrow{AN}=\overrightarrow{AP}+\overrightarrow{PN}=\overrightarrow{AP}+\lambda\overrightarrow{PB}=( - 1,0,2)+\lambda(0,\sqrt{3}, - 2)=( - 1,\sqrt{3}\lambda,2 - 2\lambda)\). 若\(AN\parallel\)平面\(BDM\),则\(\overrightarrow{AN}\cdot\boldsymbol{n}=6 + 6\lambda-15(2 - 2\lambda)= - 24 + 36\lambda = 0\), 解得\(\lambda=\frac{2}{3}\). 所以在棱PB上存在点N,使\(AN\parallel\)平面\(BDM\),此时\(\frac{PN}{PB}=\frac{2}{3}\).
3. [2023·江苏南京金陵中学高三月考]如图,在四棱锥 P - ABCD 中,PA⊥平面 ABCD,AB⊥AD,AB//CD,AB = AD = PA = 2CD = 4,G 为 PD 的中点.
(1)求证:AG⊥平面 PCD.
(2)若点 F 为 PB 的中点,线段 PC 上是否存在一点 H,使得平面 GHF⊥平面 PCD?若存在,请确定点 H 的位置;若不存在,请说明理由.
(1)求证:AG⊥平面 PCD.
(2)若点 F 为 PB 的中点,线段 PC 上是否存在一点 H,使得平面 GHF⊥平面 PCD?若存在,请确定点 H 的位置;若不存在,请说明理由.
答案:
(1)【证明】因为\(PA\perp\)平面\(ABCD\),所以\(PA\perp AB\). 又\(AD\perp AB\),\(AD\cap PA = A\),所以\(AB\perp\)平面\(PAD\). 又\(AB\parallel CD\),所以\(CD\perp\)平面\(PAD\). 因为\(AG\subset\)平面\(PAD\),所以\(CD\perp AG\). 又\(PA = AD\),G为PD的中点,所以\(AG\perp PD\). 又\(PD\cap DC = D\),所以\(AG\perp\)平面\(PCD\).
(2)【解】以A为原点,\(\overrightarrow{AD}\),\(\overrightarrow{AB}\),\(\overrightarrow{AP}\)所在方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,如图, 则\(A(0,0,0)\),\(C(4,2,0)\),\(P(0,0,4)\),\(F(0,2,2)\),\(G(2,0,2)\). 所以\(\overrightarrow{PC}=(4,2, - 4)\). 设\(\overrightarrow{PH}=k\overrightarrow{PC}(0\leqslant k\leqslant1)\)(在棱上探寻一点满足各种条件时,一般应用向量共线定理求未知点的坐标,用含参数的式子表示点的坐标时,需要注意参数的取值范围), 所以\(\overrightarrow{PH}=(4k,2k, - 4k)\), 所以\(H(4k,2k, - 4k + 4)\), 所以\(\overrightarrow{GH}=(4k - 2,2k, - 4k + 2)\),\(\overrightarrow{FG}=(2, - 2,0)\). 设平面GHF的法向量为\(\boldsymbol{n}=(x,y,z)\),则\(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{GH}=0\\\boldsymbol{n}\cdot\overrightarrow{FG}=0\end{cases}\), 即\(\begin{cases}(4k - 2)x+2ky+( - 4k + 2)z = 0\\2x - 2y = 0\end{cases}\). 令\(x = 2k - 1\),则\(\boldsymbol{n}=(2k - 1,2k - 1,3k - 1)\). 由
(1)可知\(\overrightarrow{AG}=(2,0,2)\)为平面PCD的一个法向量. 若平面\(GHF\perp\)平面\(PCD\),则\(\boldsymbol{n}\cdot\overrightarrow{AG}=0\), 即\(2k - 1+3k - 1 = 0\),解得\(k=\frac{2}{5}\). 所以线段PC上存在一点H,使得平面\(GHF\perp\)平面\(PCD\),此时\(PH=\frac{2}{5}PC\).

(1)【证明】因为\(PA\perp\)平面\(ABCD\),所以\(PA\perp AB\). 又\(AD\perp AB\),\(AD\cap PA = A\),所以\(AB\perp\)平面\(PAD\). 又\(AB\parallel CD\),所以\(CD\perp\)平面\(PAD\). 因为\(AG\subset\)平面\(PAD\),所以\(CD\perp AG\). 又\(PA = AD\),G为PD的中点,所以\(AG\perp PD\). 又\(PD\cap DC = D\),所以\(AG\perp\)平面\(PCD\).
(2)【解】以A为原点,\(\overrightarrow{AD}\),\(\overrightarrow{AB}\),\(\overrightarrow{AP}\)所在方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,如图, 则\(A(0,0,0)\),\(C(4,2,0)\),\(P(0,0,4)\),\(F(0,2,2)\),\(G(2,0,2)\). 所以\(\overrightarrow{PC}=(4,2, - 4)\). 设\(\overrightarrow{PH}=k\overrightarrow{PC}(0\leqslant k\leqslant1)\)(在棱上探寻一点满足各种条件时,一般应用向量共线定理求未知点的坐标,用含参数的式子表示点的坐标时,需要注意参数的取值范围), 所以\(\overrightarrow{PH}=(4k,2k, - 4k)\), 所以\(H(4k,2k, - 4k + 4)\), 所以\(\overrightarrow{GH}=(4k - 2,2k, - 4k + 2)\),\(\overrightarrow{FG}=(2, - 2,0)\). 设平面GHF的法向量为\(\boldsymbol{n}=(x,y,z)\),则\(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{GH}=0\\\boldsymbol{n}\cdot\overrightarrow{FG}=0\end{cases}\), 即\(\begin{cases}(4k - 2)x+2ky+( - 4k + 2)z = 0\\2x - 2y = 0\end{cases}\). 令\(x = 2k - 1\),则\(\boldsymbol{n}=(2k - 1,2k - 1,3k - 1)\). 由
(1)可知\(\overrightarrow{AG}=(2,0,2)\)为平面PCD的一个法向量. 若平面\(GHF\perp\)平面\(PCD\),则\(\boldsymbol{n}\cdot\overrightarrow{AG}=0\), 即\(2k - 1+3k - 1 = 0\),解得\(k=\frac{2}{5}\). 所以线段PC上存在一点H,使得平面\(GHF\perp\)平面\(PCD\),此时\(PH=\frac{2}{5}PC\).

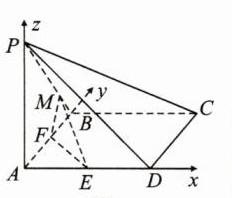
4. (原创)如图,四棱锥 P - ABCD 的底面为正方形,PA⊥底面 ABCD,PA = AB,E 为 AD 的中点,F 在线段 AB 上.
(1)在线段 PB 上是否存在一点 M,使得 PC⊥平面 EFM?若存在,请求出 PM/MB 的值;若不存在,请说明理由.
(2)在(1)的条件下,求二面角 E - MF - B 的正弦值.
(1)在线段 PB 上是否存在一点 M,使得 PC⊥平面 EFM?若存在,请求出 PM/MB 的值;若不存在,请说明理由.
(2)在(1)的条件下,求二面角 E - MF - B 的正弦值.
答案:
【解】
(1)方法一 假设存在这样一点M.连接AC,BD,如图
(1). \(\because PA\perp\)平面\(ABCD\),\(EF\),\(BD\),\(BC\subset\)平面\(ABCD\), \(\therefore PA\perp EF\),\(PA\perp BD\),\(PA\perp BC\). \(\because\)在正方形ABCD中,\(AC\perp BD\),又\(AC\cap PA = A\), \(\therefore BD\perp\)平面\(APC\). \(\because PC\perp\)平面\(EFM\),\(EF\),\(MF\subset\)平面\(EFM\), \(\therefore PC\perp MF\),\(PC\perp EF\). \(\because PA\perp EF\),\(PA\cap PC = P\),\(\therefore EF\perp\)平面\(APC\). 又\(\because BD\perp\)平面\(APC\),\(\therefore BD\parallel EF\). \(\because\)点E是AD的中点,\(\therefore\)点F是AB的中点. \(\because PA\perp BC\),\(AB\perp BC\),\(PA\cap AB = A\),\(\therefore BC\perp\)平面\(PAB\). 又\(\because MF\subset\)平面\(PAB\),\(\therefore BC\perp MF\). \(\because PC\perp MF\),\(BC\cap PC = C\),\(\therefore MF\perp\)平面\(PBC\). 又\(\because PB\subset\)平面\(PBC\),\(\therefore MF\perp PB\). \(\because PA = AB\),\(PA\perp AB\),\(\therefore PB=\sqrt{2}AB\),\(\angle PBA = 45^{\circ}\). \(\because BF=\frac{1}{2}AB\),\(\therefore MB=\frac{\sqrt{2}}{2}BF=\frac{\sqrt{2}}{4}AB\), \(\therefore\frac{PM}{MB}=\frac{PB - MB}{MB}=3\). \(\therefore\)在线段PB上存在一点M,且当\(\frac{PM}{MB}=3\)时,使得\(PC\perp\)平面\(EFM\). 方法二 由题意易知\(PA\perp AB\),\(PA\perp AD\),\(AB\perp AD\). 以A为坐标原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立如图
(2)的空间直角坐标系.设\(PA = AB = AD = 4\),则\(A(0,0,0)\),\(E(2,0,0)\),\(P(0,0,4)\),\(B(0,4,0)\),\(C(4,4,0)\),\(\overrightarrow{PC}=(4,4, - 4)\). 设\(\overrightarrow{PM}=\lambda\overrightarrow{MB}(\lambda\gt0)\), 则\(M(0,\frac{4\lambda}{1 + \lambda},\frac{4}{1 + \lambda})\), \(\therefore\overrightarrow{EM}=(-2,\frac{4\lambda}{1 + \lambda},\frac{4}{1 + \lambda})\). 设\(F(0,\mu,0)(0\leqslant\mu\leqslant4)\),则\(\overrightarrow{EF}=(-2,\mu,0)\). 要使\(PC\perp\)平面\(EFM\),只需\(\begin{cases}\overrightarrow{EM}\cdot\overrightarrow{PC}=0\\\overrightarrow{EF}\cdot\overrightarrow{PC}=0\end{cases}\), 即\(\begin{cases}-8+\frac{16\lambda}{1 + \lambda}-\frac{16}{1 + \lambda}=0\\-8 + 4\mu = 0\end{cases}\). 解得\(\begin{cases}\lambda = 3\\\mu = 2\end{cases}\),符合题意.\(\therefore\frac{PM}{MB}=3\).
(2)由题意易知\(PA\perp AB\),\(PA\perp AD\),\(AB\perp AD\). 以A为坐标原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立如图
(3)的空间直角坐标系. 设\(PA = AB = AD = 4\),则\(A(0,0,0)\),\(E(2,0,0)\),\(P(0,0,4)\),\(B(0,4,0)\),\(C(4,4,0)\),\(D(4,0,0)\),\(\overrightarrow{PC}=(4,4, - 4)\). 由
(1)可知平面EMF的一个法向量为\(\overrightarrow{PC}=(4,4, - 4)\),平面MFB的一个法向量为\(\overrightarrow{AD}=(4,0,0)\). 设二面角\(E - MF - B\)为\(\theta\), 则\(\cos\theta=\cos\langle\overrightarrow{PC},\overrightarrow{AD}\rangle=\frac{\overrightarrow{PC}\cdot\overrightarrow{AD}}{\vert\overrightarrow{PC}\vert\vert\overrightarrow{AD}\vert}=\frac{16}{4\sqrt{3}\times4}=\frac{\sqrt{3}}{3}\), 则\(\sin\theta=\sqrt{1-\cos^{2}\theta}=\frac{\sqrt{6}}{3}\). \(\therefore\)二面角\(E - MF - B\)的正弦值为\(\frac{\sqrt{6}}{3}\).
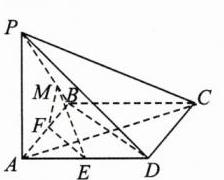
【解】
(1)方法一 假设存在这样一点M.连接AC,BD,如图
(1). \(\because PA\perp\)平面\(ABCD\),\(EF\),\(BD\),\(BC\subset\)平面\(ABCD\), \(\therefore PA\perp EF\),\(PA\perp BD\),\(PA\perp BC\). \(\because\)在正方形ABCD中,\(AC\perp BD\),又\(AC\cap PA = A\), \(\therefore BD\perp\)平面\(APC\). \(\because PC\perp\)平面\(EFM\),\(EF\),\(MF\subset\)平面\(EFM\), \(\therefore PC\perp MF\),\(PC\perp EF\). \(\because PA\perp EF\),\(PA\cap PC = P\),\(\therefore EF\perp\)平面\(APC\). 又\(\because BD\perp\)平面\(APC\),\(\therefore BD\parallel EF\). \(\because\)点E是AD的中点,\(\therefore\)点F是AB的中点. \(\because PA\perp BC\),\(AB\perp BC\),\(PA\cap AB = A\),\(\therefore BC\perp\)平面\(PAB\). 又\(\because MF\subset\)平面\(PAB\),\(\therefore BC\perp MF\). \(\because PC\perp MF\),\(BC\cap PC = C\),\(\therefore MF\perp\)平面\(PBC\). 又\(\because PB\subset\)平面\(PBC\),\(\therefore MF\perp PB\). \(\because PA = AB\),\(PA\perp AB\),\(\therefore PB=\sqrt{2}AB\),\(\angle PBA = 45^{\circ}\). \(\because BF=\frac{1}{2}AB\),\(\therefore MB=\frac{\sqrt{2}}{2}BF=\frac{\sqrt{2}}{4}AB\), \(\therefore\frac{PM}{MB}=\frac{PB - MB}{MB}=3\). \(\therefore\)在线段PB上存在一点M,且当\(\frac{PM}{MB}=3\)时,使得\(PC\perp\)平面\(EFM\). 方法二 由题意易知\(PA\perp AB\),\(PA\perp AD\),\(AB\perp AD\). 以A为坐标原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立如图
(2)的空间直角坐标系.设\(PA = AB = AD = 4\),则\(A(0,0,0)\),\(E(2,0,0)\),\(P(0,0,4)\),\(B(0,4,0)\),\(C(4,4,0)\),\(\overrightarrow{PC}=(4,4, - 4)\). 设\(\overrightarrow{PM}=\lambda\overrightarrow{MB}(\lambda\gt0)\), 则\(M(0,\frac{4\lambda}{1 + \lambda},\frac{4}{1 + \lambda})\), \(\therefore\overrightarrow{EM}=(-2,\frac{4\lambda}{1 + \lambda},\frac{4}{1 + \lambda})\). 设\(F(0,\mu,0)(0\leqslant\mu\leqslant4)\),则\(\overrightarrow{EF}=(-2,\mu,0)\). 要使\(PC\perp\)平面\(EFM\),只需\(\begin{cases}\overrightarrow{EM}\cdot\overrightarrow{PC}=0\\\overrightarrow{EF}\cdot\overrightarrow{PC}=0\end{cases}\), 即\(\begin{cases}-8+\frac{16\lambda}{1 + \lambda}-\frac{16}{1 + \lambda}=0\\-8 + 4\mu = 0\end{cases}\). 解得\(\begin{cases}\lambda = 3\\\mu = 2\end{cases}\),符合题意.\(\therefore\frac{PM}{MB}=3\).
(2)由题意易知\(PA\perp AB\),\(PA\perp AD\),\(AB\perp AD\). 以A为坐标原点,AD,AB,AP所在直线分别为x轴、y轴、z轴建立如图
(3)的空间直角坐标系. 设\(PA = AB = AD = 4\),则\(A(0,0,0)\),\(E(2,0,0)\),\(P(0,0,4)\),\(B(0,4,0)\),\(C(4,4,0)\),\(D(4,0,0)\),\(\overrightarrow{PC}=(4,4, - 4)\). 由
(1)可知平面EMF的一个法向量为\(\overrightarrow{PC}=(4,4, - 4)\),平面MFB的一个法向量为\(\overrightarrow{AD}=(4,0,0)\). 设二面角\(E - MF - B\)为\(\theta\), 则\(\cos\theta=\cos\langle\overrightarrow{PC},\overrightarrow{AD}\rangle=\frac{\overrightarrow{PC}\cdot\overrightarrow{AD}}{\vert\overrightarrow{PC}\vert\vert\overrightarrow{AD}\vert}=\frac{16}{4\sqrt{3}\times4}=\frac{\sqrt{3}}{3}\), 则\(\sin\theta=\sqrt{1-\cos^{2}\theta}=\frac{\sqrt{6}}{3}\). \(\therefore\)二面角\(E - MF - B\)的正弦值为\(\frac{\sqrt{6}}{3}\).


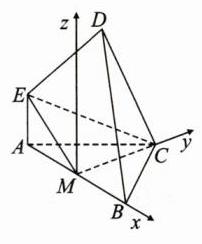
5. [2023·河南安阳一中高二阶段检测]在如图所示的多面体中,EA⊥平面 ABC,DB⊥平面 ABC,AC⊥BC,且 AC = BC = BD = 2AE = 2,M 是 AB 的中点.
(1)求证:CM⊥EM.
(2)在棱 DC 上是否存在一点 N,使直线 MN 与平面 EMC 所成的角是 60°?若存在,指出点 N 的位置;若不存在,请说明理由.
(1)求证:CM⊥EM.
(2)在棱 DC 上是否存在一点 N,使直线 MN 与平面 EMC 所成的角是 60°?若存在,指出点 N 的位置;若不存在,请说明理由.
答案:
(1)【证明】\(\because AC = BC\),M是AB的中点, \(\therefore CM\perp AB\). 又\(EA\perp\)平面\(ABC\),\(CM\subset\)平面\(ABC\),\(\therefore CM\perp EA\). \(\because EA\cap AB = A\),\(EA\subset\)平面\(AEM\),\(AB\subset\)平面\(AEM\), \(\therefore CM\perp\)平面\(AEM\). \(\because EM\subset\)平面\(AEM\),\(\therefore CM\perp EM\).
(2)【解】以M为原点,分别以MB,MC所在直线为x轴、y轴,过点M且平行于AE的直线为z轴,建立空间直角坐标系,如图, 则\(M(0,0,0)\),\(C(0,\sqrt{2},0)\),\(B(\sqrt{2},0,0)\),\(D(\sqrt{2},0,2)\),\(E(-\sqrt{2},0,1)\), 所以\(\overrightarrow{ME}=(-\sqrt{2},0,1)\),\(\overrightarrow{MC}=(0,\sqrt{2},0)\),\(\overrightarrow{BD}=(0,0,2)\),\(\overrightarrow{BC}=(-\sqrt{2},\sqrt{2},0)\). 设平面EMC的法向量为\(\boldsymbol{m}=(x_{1},y_{1},z_{1})\),则 \(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{ME}=0\\\boldsymbol{m}\cdot\overrightarrow{MC}=0\end{cases}\),即\(\begin{cases}-\sqrt{2}x_{1}+z_{1}=0\\\sqrt{2}y_{1}=0\end{cases}\). 不妨取\(x_{1}=1\),则\(y_{1}=0\),\(z_{1}=\sqrt{2}\),所以\(\boldsymbol{m}=(1,0,\sqrt{2})\). 假设在棱DC上存在一点N,使直线MN与平面EMC所成的角是\(60^{\circ}\). 设\(N(x,y,z)\)且\(\overrightarrow{DN}=\lambda\overrightarrow{DC}(0\leqslant\lambda\leqslant1)\), \(\therefore(x - \sqrt{2},y,z - 2)=\lambda(-\sqrt{2},\sqrt{2}, - 2)\), \(\therefore x=\sqrt{2}-\sqrt{2}\lambda\),\(y=\sqrt{2}\lambda\),\(z = 2 - 2\lambda\), \(\therefore\overrightarrow{MN}=(\sqrt{2}-\sqrt{2}\lambda,\sqrt{2}\lambda,2 - 2\lambda)\). 若直线MN与平面EMC所成的角为\(60^{\circ}\),则 \(\vert\cos\langle\overrightarrow{MN},\boldsymbol{m}\rangle\vert=\frac{\vert\sqrt{2}-\sqrt{2}\lambda+\sqrt{2}(2 - 2\lambda)\vert}{\sqrt{3}\times\sqrt{2(1 - \lambda)^{2}+2\lambda^{2}+4(1 - \lambda)^{2}}}=\sin60^{\circ}=\frac{\sqrt{3}}{2}\),解得\(\lambda=\frac{1}{2}\). \(\therefore\)点N为棱DC的中点. \(\therefore\)在棱DC上存在一点N,使直线MN与平面EMC所成的角是\(60^{\circ}\),此时点N为DC的中点.
(1)【证明】\(\because AC = BC\),M是AB的中点, \(\therefore CM\perp AB\). 又\(EA\perp\)平面\(ABC\),\(CM\subset\)平面\(ABC\),\(\therefore CM\perp EA\). \(\because EA\cap AB = A\),\(EA\subset\)平面\(AEM\),\(AB\subset\)平面\(AEM\), \(\therefore CM\perp\)平面\(AEM\). \(\because EM\subset\)平面\(AEM\),\(\therefore CM\perp EM\).
(2)【解】以M为原点,分别以MB,MC所在直线为x轴、y轴,过点M且平行于AE的直线为z轴,建立空间直角坐标系,如图, 则\(M(0,0,0)\),\(C(0,\sqrt{2},0)\),\(B(\sqrt{2},0,0)\),\(D(\sqrt{2},0,2)\),\(E(-\sqrt{2},0,1)\), 所以\(\overrightarrow{ME}=(-\sqrt{2},0,1)\),\(\overrightarrow{MC}=(0,\sqrt{2},0)\),\(\overrightarrow{BD}=(0,0,2)\),\(\overrightarrow{BC}=(-\sqrt{2},\sqrt{2},0)\). 设平面EMC的法向量为\(\boldsymbol{m}=(x_{1},y_{1},z_{1})\),则 \(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{ME}=0\\\boldsymbol{m}\cdot\overrightarrow{MC}=0\end{cases}\),即\(\begin{cases}-\sqrt{2}x_{1}+z_{1}=0\\\sqrt{2}y_{1}=0\end{cases}\). 不妨取\(x_{1}=1\),则\(y_{1}=0\),\(z_{1}=\sqrt{2}\),所以\(\boldsymbol{m}=(1,0,\sqrt{2})\). 假设在棱DC上存在一点N,使直线MN与平面EMC所成的角是\(60^{\circ}\). 设\(N(x,y,z)\)且\(\overrightarrow{DN}=\lambda\overrightarrow{DC}(0\leqslant\lambda\leqslant1)\), \(\therefore(x - \sqrt{2},y,z - 2)=\lambda(-\sqrt{2},\sqrt{2}, - 2)\), \(\therefore x=\sqrt{2}-\sqrt{2}\lambda\),\(y=\sqrt{2}\lambda\),\(z = 2 - 2\lambda\), \(\therefore\overrightarrow{MN}=(\sqrt{2}-\sqrt{2}\lambda,\sqrt{2}\lambda,2 - 2\lambda)\). 若直线MN与平面EMC所成的角为\(60^{\circ}\),则 \(\vert\cos\langle\overrightarrow{MN},\boldsymbol{m}\rangle\vert=\frac{\vert\sqrt{2}-\sqrt{2}\lambda+\sqrt{2}(2 - 2\lambda)\vert}{\sqrt{3}\times\sqrt{2(1 - \lambda)^{2}+2\lambda^{2}+4(1 - \lambda)^{2}}}=\sin60^{\circ}=\frac{\sqrt{3}}{2}\),解得\(\lambda=\frac{1}{2}\). \(\therefore\)点N为棱DC的中点. \(\therefore\)在棱DC上存在一点N,使直线MN与平面EMC所成的角是\(60^{\circ}\),此时点N为DC的中点.

6. [2023·江苏常州横林高级中学高二月考]如图,正方体 ABCD - A₁B₁C₁D₁ 的棱长为 2,E,F 分别为 BD 和 BB₁ 的中点,P 为棱 C₁D₁ 上的动点.
(1)是否存在点 P,使 PE⊥平面 EFC?若存在,求出满足条件时 C₁P 的长度;若不存在,请说明理由.
(2)当 C₁P 为何值时,平面 BCC₁B₁ 与平面 PEF 所成锐二面角的正弦值最小?
(1)是否存在点 P,使 PE⊥平面 EFC?若存在,求出满足条件时 C₁P 的长度;若不存在,请说明理由.
(2)当 C₁P 为何值时,平面 BCC₁B₁ 与平面 PEF 所成锐二面角的正弦值最小?
答案:
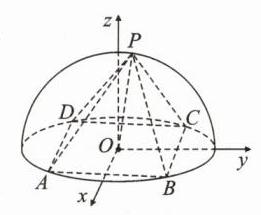
7. [2021·山西临汾高三二模]如图,在半径为√3的半球 O 中,平行四边形 ABCD 是圆 O 的内接四边形,AD = √2AB,点 P 是半球面上的动点,且四棱锥 P - ABCD 的体积为 $\frac{8}{3.}$
(1)求动点 P 的轨迹 T 围成的图形的面积.
(2)是否存在点 P 使得二面角 P - AD - B 的大小为 π/3?请说明理由.
(1)求动点 P 的轨迹 T 围成的图形的面积.
(2)是否存在点 P 使得二面角 P - AD - B 的大小为 π/3?请说明理由.
答案:
【解】
(1)依题意,建立如图所示的空间直角坐标系, 则\(E(1,1,0)\),\(F(2,2,1)\),\(C(0,2,0)\),\(C_{1}(0,2,2)\). 设\(P(0,t,2)\),\(0\leqslant t\leqslant2\),则\(\overrightarrow{CE}=(1, - 1,0)\),\(\overrightarrow{CF}=(2,0,1)\),\(\overrightarrow{PE}=(1,1 - t, - 2)\). 所以\(\overrightarrow{CF}\cdot\overrightarrow{PE}=0\),所以\(PE\perp CF\). 令\(\overrightarrow{CE}\cdot\overrightarrow{PE}=1 + t - 1 = 0\),得\(t = 0\), 此时\(PE\perp CE\). 因为\(CE\cap CF = C\),且\(CE\),\(CF\subset\)平面\(CEF\), 所以\(PE\perp\)平面\(EFC\). 所以存在点\(P(0,0,2)\),使\(PE\perp\)平面\(EFC\),此时\(C_{1}P = 2\).
(2)由
(1)得\(\overrightarrow{EF}=(1,1,1)\),\(\overrightarrow{PE}=(1,1 - t, - 2)\). 设平面PEF的法向量为\(\boldsymbol{n}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{EF}=x + y + z = 0\\\boldsymbol{n}\cdot\overrightarrow{PE}=x+(1 - t)y - 2z = 0\end{cases}\). 取\(y = 3\),则\(x = t - 3\),\(z = - t\),所以\(\boldsymbol{n}=(t - 3,3, - t)\). 易知平面\(BCC_{1}B_{1}\)的一个法向量为\(\boldsymbol{m}=(0,1,0)\). 设平面\(BCC_{1}B_{1}\)与平面\(PEF\)所成的锐二面角为\(\theta\), 则\(\cos\theta=\frac{\vert\boldsymbol{m}\cdot\boldsymbol{n}\vert}{\vert\boldsymbol{m}\vert\vert\boldsymbol{n}\vert}=\frac{3}{\sqrt{(t - 3)^{2}+9 + t^{2}}}=\frac{3}{\sqrt{2(t-\frac{3}{2})^{2}+\frac{27}{2}}}\leqslant\frac{\sqrt{6}}{3}\),当且仅当\(t=\frac{3}{2}\)时等号成立. 所以当\(t=\frac{3}{2}\),即\(P(0,\frac{3}{2},2)\)时,\(\cos\theta\)取得最大值\(\frac{\sqrt{6}}{3}\), 所以\(\sin\theta=\sqrt{1-\cos^{2}\theta}\geqslant\frac{\sqrt{3}}{3}\),当且仅当\(\cos\theta=\frac{\sqrt{6}}{3}\)时等号成立, 所以当\(P(0,\frac{3}{2},2)\),即\(C_{1}P=\frac{1}{2}\)时,平面\(BCC_{1}B_{1}\)与平面\(PEF\)所成锐二面角的正弦值最小.
【解】
(1)依题意,建立如图所示的空间直角坐标系, 则\(E(1,1,0)\),\(F(2,2,1)\),\(C(0,2,0)\),\(C_{1}(0,2,2)\). 设\(P(0,t,2)\),\(0\leqslant t\leqslant2\),则\(\overrightarrow{CE}=(1, - 1,0)\),\(\overrightarrow{CF}=(2,0,1)\),\(\overrightarrow{PE}=(1,1 - t, - 2)\). 所以\(\overrightarrow{CF}\cdot\overrightarrow{PE}=0\),所以\(PE\perp CF\). 令\(\overrightarrow{CE}\cdot\overrightarrow{PE}=1 + t - 1 = 0\),得\(t = 0\), 此时\(PE\perp CE\). 因为\(CE\cap CF = C\),且\(CE\),\(CF\subset\)平面\(CEF\), 所以\(PE\perp\)平面\(EFC\). 所以存在点\(P(0,0,2)\),使\(PE\perp\)平面\(EFC\),此时\(C_{1}P = 2\).
(2)由
(1)得\(\overrightarrow{EF}=(1,1,1)\),\(\overrightarrow{PE}=(1,1 - t, - 2)\). 设平面PEF的法向量为\(\boldsymbol{n}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{EF}=x + y + z = 0\\\boldsymbol{n}\cdot\overrightarrow{PE}=x+(1 - t)y - 2z = 0\end{cases}\). 取\(y = 3\),则\(x = t - 3\),\(z = - t\),所以\(\boldsymbol{n}=(t - 3,3, - t)\). 易知平面\(BCC_{1}B_{1}\)的一个法向量为\(\boldsymbol{m}=(0,1,0)\). 设平面\(BCC_{1}B_{1}\)与平面\(PEF\)所成的锐二面角为\(\theta\), 则\(\cos\theta=\frac{\vert\boldsymbol{m}\cdot\boldsymbol{n}\vert}{\vert\boldsymbol{m}\vert\vert\boldsymbol{n}\vert}=\frac{3}{\sqrt{(t - 3)^{2}+9 + t^{2}}}=\frac{3}{\sqrt{2(t-\frac{3}{2})^{2}+\frac{27}{2}}}\leqslant\frac{\sqrt{6}}{3}\),当且仅当\(t=\frac{3}{2}\)时等号成立. 所以当\(t=\frac{3}{2}\),即\(P(0,\frac{3}{2},2)\)时,\(\cos\theta\)取得最大值\(\frac{\sqrt{6}}{3}\), 所以\(\sin\theta=\sqrt{1-\cos^{2}\theta}\geqslant\frac{\sqrt{3}}{3}\),当且仅当\(\cos\theta=\frac{\sqrt{6}}{3}\)时等号成立, 所以当\(P(0,\frac{3}{2},2)\),即\(C_{1}P=\frac{1}{2}\)时,平面\(BCC_{1}B_{1}\)与平面\(PEF\)所成锐二面角的正弦值最小.

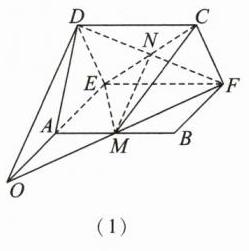
8. [2022·山东德州第一中学高二期末]如图(1),正方形 ABCD 的边长为 2,E,F 分别为 AD,BC 的中点,将 ABCD 沿 EF 折成如图(2)所示的二面角,且二面角的大小为 60°,点 M 在线段 AB 上(包含端点)运动,连接 AD.
(1)若 M 为 AB 的中点,直线 MF 与平面 ADE 的交点为 O,试确定点 O 的位置,并证明直线 OD//平面 EMC.
(2)是否存在点 M,使直线 DE 与平面 EMC 所成的角为 60°?若存在,求此时 AM 的长;若不存在,请说明理由.
(1)若 M 为 AB 的中点,直线 MF 与平面 ADE 的交点为 O,试确定点 O 的位置,并证明直线 OD//平面 EMC.
(2)是否存在点 M,使直线 DE 与平面 EMC 所成的角为 60°?若存在,求此时 AM 的长;若不存在,请说明理由.
答案:
【解】
(1)因为直线\(MF\subset\)平面\(ABFE\),所以点O在平面\(ABFE\)内,也在平面\(ADE\)内, 所以点O在平面\(ABFE\)与平面\(ADE\)的交线即直线AE上. 延长EA,FM交于点O,连接OD,如图
(1). 因为\(AO\parallel BF\),M为AB的中点,即\(AM = BM\), 所以\(\triangle OAM\cong\triangle FBM\). 所以\(OM = MF\),\(AO = FB = 1\). 故点O在EA的延长线上且与点A的距离为1. 连接DF,交EC于点N. 因为四边形CDEF为矩形,所以N是EC的中点. 连接MN,则MN为\(\triangle DOF\)的中位线,所以\(MN\parallel OD\). 又\(MN\subset\)平面\(EMC\),\(OD\not\subset\)平面\(EMC\), 所以直线\(OD\parallel\)平面\(EMC\).
(2)由已知条件可得\(EF\perp AE\),\(EF\perp DE\). 又\(AE\cap DE = E\),所以\(EF\perp\)平面\(ADE\). 因为\(EF\subset\)平面\(ABFE\),所以平面\(ABFE\perp\)平面\(ADE\). 由题意可知\(\angle DEA = 60^{\circ}\),又\(ED = EA\), 所以\(\triangle ADE\)为等边三角形. 取AE的中点H,连接DH,如图
(2),则\(DH\perp AE\). 因为平面\(ABFE\cap\)平面\(ADE = AE\),\(DH\subset\)平面\(ADE\), 所以\(DH\perp\)平面\(ABFE\). 以H为原点建立如图所示的空间直角坐标系, 则\(E(-\frac{1}{2},0,0)\),\(D(0,0,\frac{\sqrt{3}}{2})\),\(C(0,2,\frac{\sqrt{3}}{2})\),\(F(-\frac{1}{2},2,0)\), 所以\(\overrightarrow{DE}=(-\frac{1}{2},0,-\frac{\sqrt{3}}{2})\),\(\overrightarrow{EC}=(\frac{1}{2},2,\frac{\sqrt{3}}{2})\). 设\(M(\frac{1}{2},a,0)(0\leqslant a\leqslant2)\),则\(\overrightarrow{EM}=(1,a,0)\). 设平面EMC的法向量为\(\boldsymbol{m}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{EM}=x + ay = 0\\\boldsymbol{m}\cdot\overrightarrow{EC}=\frac{1}{2}x + 2y+\frac{\sqrt{3}}{2}z = 0\end{cases}\). 取\(y = -\sqrt{3}\),得\(\boldsymbol{m}=(\sqrt{3}a,-\sqrt{3},4 - a)\). 要使直线DE与平面EMC所成的角为\(60^{\circ}\), 则\(\vert\cos\langle\overrightarrow{DE},\boldsymbol{m}\rangle\vert=\frac{\vert\overrightarrow{DE}\cdot\boldsymbol{m}\vert}{\vert\overrightarrow{DE}\vert\vert\boldsymbol{m}\vert}=\frac{\vert-\frac{1}{2}\times\sqrt{3}a+0\times(-\sqrt{3})+(-\frac{\sqrt{3}}{2})\times(4 - a)\vert}{\sqrt{(-\frac{1}{2})^{2}+0^{2}+(-\frac{\sqrt{3}}{2})^{2}}\times\sqrt{(\sqrt{3}a)^{2}+(-\sqrt{3})^{2}+(4 - a)^{2}}}=\frac{2\sqrt{3}}{\sqrt{4a^{2}-8a + 19}}=\frac{\sqrt{3}}{2}\), 解得\(a=\frac{1}{2}\)或\(a=\frac{3}{2}\). 所以存在点M,使直线DE与平面EMC所成的角为\(60^{\circ}\),此时\(AM=\frac{1}{2}\)或\(AM=\frac{3}{2}\).

【解】
(1)因为直线\(MF\subset\)平面\(ABFE\),所以点O在平面\(ABFE\)内,也在平面\(ADE\)内, 所以点O在平面\(ABFE\)与平面\(ADE\)的交线即直线AE上. 延长EA,FM交于点O,连接OD,如图
(1). 因为\(AO\parallel BF\),M为AB的中点,即\(AM = BM\), 所以\(\triangle OAM\cong\triangle FBM\). 所以\(OM = MF\),\(AO = FB = 1\). 故点O在EA的延长线上且与点A的距离为1. 连接DF,交EC于点N. 因为四边形CDEF为矩形,所以N是EC的中点. 连接MN,则MN为\(\triangle DOF\)的中位线,所以\(MN\parallel OD\). 又\(MN\subset\)平面\(EMC\),\(OD\not\subset\)平面\(EMC\), 所以直线\(OD\parallel\)平面\(EMC\).
(2)由已知条件可得\(EF\perp AE\),\(EF\perp DE\). 又\(AE\cap DE = E\),所以\(EF\perp\)平面\(ADE\). 因为\(EF\subset\)平面\(ABFE\),所以平面\(ABFE\perp\)平面\(ADE\). 由题意可知\(\angle DEA = 60^{\circ}\),又\(ED = EA\), 所以\(\triangle ADE\)为等边三角形. 取AE的中点H,连接DH,如图
(2),则\(DH\perp AE\). 因为平面\(ABFE\cap\)平面\(ADE = AE\),\(DH\subset\)平面\(ADE\), 所以\(DH\perp\)平面\(ABFE\). 以H为原点建立如图所示的空间直角坐标系, 则\(E(-\frac{1}{2},0,0)\),\(D(0,0,\frac{\sqrt{3}}{2})\),\(C(0,2,\frac{\sqrt{3}}{2})\),\(F(-\frac{1}{2},2,0)\), 所以\(\overrightarrow{DE}=(-\frac{1}{2},0,-\frac{\sqrt{3}}{2})\),\(\overrightarrow{EC}=(\frac{1}{2},2,\frac{\sqrt{3}}{2})\). 设\(M(\frac{1}{2},a,0)(0\leqslant a\leqslant2)\),则\(\overrightarrow{EM}=(1,a,0)\). 设平面EMC的法向量为\(\boldsymbol{m}=(x,y,z)\), 则\(\begin{cases}\boldsymbol{m}\cdot\overrightarrow{EM}=x + ay = 0\\\boldsymbol{m}\cdot\overrightarrow{EC}=\frac{1}{2}x + 2y+\frac{\sqrt{3}}{2}z = 0\end{cases}\). 取\(y = -\sqrt{3}\),得\(\boldsymbol{m}=(\sqrt{3}a,-\sqrt{3},4 - a)\). 要使直线DE与平面EMC所成的角为\(60^{\circ}\), 则\(\vert\cos\langle\overrightarrow{DE},\boldsymbol{m}\rangle\vert=\frac{\vert\overrightarrow{DE}\cdot\boldsymbol{m}\vert}{\vert\overrightarrow{DE}\vert\vert\boldsymbol{m}\vert}=\frac{\vert-\frac{1}{2}\times\sqrt{3}a+0\times(-\sqrt{3})+(-\frac{\sqrt{3}}{2})\times(4 - a)\vert}{\sqrt{(-\frac{1}{2})^{2}+0^{2}+(-\frac{\sqrt{3}}{2})^{2}}\times\sqrt{(\sqrt{3}a)^{2}+(-\sqrt{3})^{2}+(4 - a)^{2}}}=\frac{2\sqrt{3}}{\sqrt{4a^{2}-8a + 19}}=\frac{\sqrt{3}}{2}\), 解得\(a=\frac{1}{2}\)或\(a=\frac{3}{2}\). 所以存在点M,使直线DE与平面EMC所成的角为\(60^{\circ}\),此时\(AM=\frac{1}{2}\)或\(AM=\frac{3}{2}\).


查看更多完整答案,请扫码查看


