2025年练习生高中数学选择性必修第一册人教A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第一册人教A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.[2022.辽宁沈阳二中高二期末]已知F,F2分别为双曲线$\frac{x}{a²}$−$\frac{y²}{62}$=1(a>0,b>0)的左、右焦点,以F,F2为直径的圆与双曲线在第一象限和第三象限的交点分别为M,N,设四边形F,NF2M的周长为p,面积为S,且满足32S=p²²,则该双曲线的离心率为 ( )
A.$\frac{3}{2}$
B.2
C.$\frac{\sqrt{6}}{2}$
D.$\sqrt{3}$
A.$\frac{3}{2}$
B.2
C.$\frac{\sqrt{6}}{2}$
D.$\sqrt{3}$
答案:
C
2.[2022.江苏南通高二期末]如图,
一只装有半杯水的圆柱形水杯,将
其倾斜使杯底与水平桌面成30°,
此时杯内水面成椭圆形,此椭圆的
离心率为 ( )
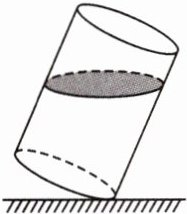
A.$\frac{√3}{2}$
B.$\frac{\sqrt{3}}{4}$
C.$\frac{1}{2}$
D.$\frac{1}{4}$
一只装有半杯水的圆柱形水杯,将
其倾斜使杯底与水平桌面成30°,
此时杯内水面成椭圆形,此椭圆的
离心率为 ( )

A.$\frac{√3}{2}$
B.$\frac{\sqrt{3}}{4}$
C.$\frac{1}{2}$
D.$\frac{1}{4}$
答案:
C
3.[2022.河南洛阳创新发展联盟高二联考]已知F1,F2分别为椭圆C:$\frac{x}{a²}$2+$\frac{y²}{62}$=1的左、右焦点,M是C 上一点,O为原点,过点F2作∠F1MF2的平分线的垂线,垂足为N,若IONI=$\frac{b}{2}$,IOMI=c,则C的离心率为 ( )
A.$\frac{1}{3}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{2}{3}$
D.$\frac{\sqrt{5}}{3}$
A.$\frac{1}{3}$
B.$\frac{\sqrt{3}}{2}$
C.$\frac{2}{3}$
D.$\frac{\sqrt{5}}{3}$
答案:
D
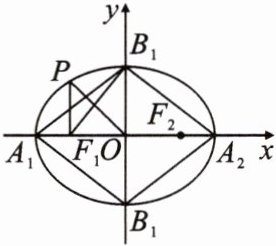
4.(多选)[2023.辽宁铁岭清河
中学高二月考]如图,已知椭
圆C:$\frac{x}{a²}$2+$\frac{y2}{62}$=1(a>b>0),A1,
A2分别为左、右顶点,B,B2分别为上、下顶点,F,F2分别为左、右焦点,点P在椭圆C上,则下列条件中能使C的离心率为$\frac{\sqrt{5}−1}{2}$的是 ( )
A.1OF,1.|0A2↓=10B,1²
有关椭圆、双曲线的离心率问题 ?答案见D89
B.∠FBA=90°
C.PF1⊥x轴,且PO//A2B1
D.四边形A,B,A2B2的内切圆过焦点F,F2
中学高二月考]如图,已知椭
圆C:$\frac{x}{a²}$2+$\frac{y2}{62}$=1(a>b>0),A1,
A2分别为左、右顶点,B,B2分别为上、下顶点,F,F2分别为左、右焦点,点P在椭圆C上,则下列条件中能使C的离心率为$\frac{\sqrt{5}−1}{2}$的是 ( )
A.1OF,1.|0A2↓=10B,1²
有关椭圆、双曲线的离心率问题 ?答案见D89
B.∠FBA=90°
C.PF1⊥x轴,且PO//A2B1
D.四边形A,B,A2B2的内切圆过焦点F,F2

答案:
ABD
5.[2022.北京陈经纶中学高二期中]已知椭圆C:$\frac{x}{a²}$2+y²=¹(a>b>0),椭圆的左、右焦点分别为F,F22,P是椭圆C上的任意一点,且满足PF.PF>0,则椭圆C的离心率e的取值范围是 ( )
A.(0,$\frac{1}{2}$ B.(0,$\frac{\sqrt{2}}{2}$ C $\frac{1}{2}$,$\frac{\sqrt{2}}{2}$ D.($\frac{\sqrt{2}}{2}$
A.(0,$\frac{1}{2}$ B.(0,$\frac{\sqrt{2}}{2}$ C $\frac{1}{2}$,$\frac{\sqrt{2}}{2}$ D.($\frac{\sqrt{2}}{2}$
答案:
B
6.(多选)[2022.河北固安一中高二月考]已知椭圆$\frac{x²}{a²}$+γ²=¹(a>b>0)上一点A关于原点的对称点为点
B,F为其右焦点.若AF⊥BF,设∠ABF=α,且α∈$\frac{H}{6}$,$\frac{H}{4}$,则该椭圆的离心率e的可能取值为( )
A.$\frac{1}{2}$ .B.$\frac{\sqrt{2}}{2}$ C.$\sqrt{3}$−1 D.$\frac{\sqrt{3}}{2}$
B,F为其右焦点.若AF⊥BF,设∠ABF=α,且α∈$\frac{H}{6}$,$\frac{H}{4}$,则该椭圆的离心率e的可能取值为( )
A.$\frac{1}{2}$ .B.$\frac{\sqrt{2}}{2}$ C.$\sqrt{3}$−1 D.$\frac{\sqrt{3}}{2}$
答案:
BC
7.[2022.四川内江六中高二月考]设F1,F2同时为椭圆C,:$\frac{x}{a?}$2+$\frac{y}{62}$2=1(a,>b,>0)与双曲线C2:$\frac{x²}{a2}$−$\frac{y²}{62}$=1(a2>0,b2>0)的左、右焦点,设椭圆C与双曲线C2在第一象限内交于点M,椭圆C1与双曲线C2的离心率分别为e1,e2,O为原点.若IF,F2l=4IMF21,则ee2的取值范围是 ( )
A.0,$\frac{2}{3}$ B.$\frac{2}{3}$,$\frac{3}{2}${
C.$\frac{2}{3}$,2 D.$\frac{2}{3}$,+∞)
A.0,$\frac{2}{3}$ B.$\frac{2}{3}$,$\frac{3}{2}${
C.$\frac{2}{3}$,2 D.$\frac{2}{3}$,+∞)
答案:
C
8.[2022.安徽宣城高二期末]已知双曲线$\frac{x}{a²}$−$\frac{y}{62}$=1 (a>0,b>0)的左、右焦点分别是F!,F2,在其渐近线上存在一点P,满足IIPF,I−IPF2II=2b,则该双曲线的离心率的取值范围是________.
答案:
$(1,\sqrt {2})$
查看更多完整答案,请扫码查看


