《2025年练习生高中数学选择性必修第一册人教A版》

12. (多选)[2022·河南商丘高二月考]已知直线$l:3x + 4y - 10 = 0$与圆$C:x^{2}+y^{2}=9$，则（ ）
A. 直线$l$与圆$C$相离
B. 直线$l$与圆$C$相交
C. 圆$C$上到直线$l$的距离为1的点共有2个
D. 圆$C$上到直线$l$的距离为1的点共有3个

答案： BD

13. 已知集合$A = \{(x,y)|x,y$为实数，且$x^{2}+y^{2}=1\}$，$B = \{(x,y)|x,y$为实数，且$x + y = 1\}$，则$A\cap B$的元素个数为（ ）
A. 4
B. 3
C. 2
D. 1

答案： C

14. 若直线$l:y = x + b$与曲线$y = \sqrt{4 - x^{2}}$有两个交点，则实数$b$的取值范围是（ ）
A. $\{b|-2\sqrt{2}＜b＜2\sqrt{2}\}$
B. $\{b|2＜b＜2\sqrt{2}\}$
C. $\{b|2\leq b＜2\sqrt{2}\}$
D. $\{b|b = \pm 2\}$

答案： C

15. [2022·山东济宁高二月考]若圆$C:x^{2}+y^{2}+2x - 4y + 3 = 0$关于直线$2ax + by + 6 = 0$对称，则由点$(a,b)$向圆所作的切线长的最小值是（ ）
A. 2
B. 3
C. 4
D. 6

答案： C

16. 台风中心从$A$地以20 km/h的速度向东北方向移动，离台风中心30 km内的地区为危险区，城市$B$在$A$地正东40 km处，则城市$B$处于危险区内的时间为（ ）
A. 0.5 h
B. 1 h
C. 1.5 h
D. 2 h

答案： B

17. 直线$l$与圆$x^{2}+y^{2}+2x - 4y + a = 0$相交于$A,B$两点. 若弦$AB$的中点为$C(-2,3)$，则$a$的取值范围是________，直线$l$的方程为________.

答案： (-∞,3)   x-y+5=0

18. 已知$AC,BD$为圆$O:x^{2}+y^{2}=4$的两条相互垂直的弦，其中垂足为$M(1,\sqrt{2})$，则四边形$ABCD$的面积的最大值为________.

答案： 5

19. [2022·安徽阜阳高二统测]圆$x^{2}+y^{2}-4x + 2y - 3 = 0$上恰好有两点到直线$x + y - a = 0$的距离为$\sqrt{2}$，则实数$a$的取值范围是________.

答案： (-5，-1)∪(3，7)

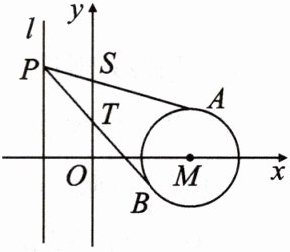
20. [2023·广东深圳红岭中学高二期中]如图，已知圆$M:x^{2}-4x + y^{2}+3 = 0$，点$P(-1,t)$为直线$l:x = -1$上一动点，过点$P$引圆$M$的两条切线，切点分别为$A,B$.
(1)求直线$AB$的方程，并写出直线$AB$所经过的定点坐标；
(2)求线段$AB$中点的轨迹方程(不必写出$x,y$的取值范围)；
(3)若两条切线$PA,PB$与$y$轴分别交于$S,T$两点，求$|ST|$的最小值.

答案： $(\frac {5}{3},0)$
(x-$\frac {11}{6}$)^{2}+y$^{2}$=$\frac {1}{36}$
$\frac {\sqrt {2}}{2}$

21. [2023·江西南昌高二联考]已知点$P(2,0)$，圆$C:x^{2}+y^{2}-6x + 4y + 4 = 0$.
(1)若直线$l$过点$P$且被圆$C$截得的弦长为$4\sqrt{2}$，求直线$l$的方程.
(2)设直线$ax - y + 1 = 0$与圆$C$交于$A,B$两点，过点$P(2,0)$的直线$l_{1}$垂直平分弦$AB$，这样的实数$a$是否存在？若存在，求出实数$a$的值；若不存在，请说明理由.

答案：
(1)3x+4y-6=0或x=2
(2)把直线方程与⊙C方程联立并消去y得$(a^{2}+1)x^{2}+6(a-1)x+9=0$
由于它们有两个交点
所以,$△=36(a-1)^{2}-36(a^{2}+1)$>0,即$-72a>0$，解得$a<0$. 设符合条件的实数$a$存在. 由于直线$l_{1}$垂直平分弦$AB$，故圆心$C(3,-2)$必在直线$l_{1}$上. 所以直线$l_{1}$的斜率$k_{PC}=-2$. 因为$k_{AB}=a=-\frac{1}{k_{PC}}$，所以$a=\frac{1}{2}$. 由于$\frac{1}{2}\notin(-\infty ,0)$，故不存在实数$a$，使过点$P(2,0)$的直线$l_{1}$垂直平分弦$AB$.