《2025年练习生高中数学选择性必修第一册人教A版》

1. [2022·江苏扬州高二期中]在平面直角坐标系中，若 x 与 y 都是整数，则称点(x,y)为整点. 有下列 5 个命题：
(1)存在这样的直线 l，既不与坐标轴平行又不经过任何整点；
(2)若 k 与 b 都是无理数，则直线 l:y = kx + b 不经过任何整点；
(3)直线 l:y = kx 经过无穷多个整点，当且仅当 l 经过两个不同的整点；
(4)直线 l:y = kx + b 经过无穷多个整点的充分必要条件是 k 与 b 都是有理数；
(5)存在恰经过一个整点的直线 l.
写出 2 个你认为正确命题的编号，并说明理由.

答案： 【解】
(1)令直线$l$为$y = x+\frac{1}{2}$，则该直线不与坐标轴平行且不经过任何整点，
(1)正确.
(2)令直线$l$为$y = \sqrt{2}x - 2\sqrt{2}$，则该直线经过整点$(2,0)$，
(2)错误.
(3)直线$l:y = kx$经过两个不同的整点$(x_1,y_1)$，$(x_2,y_2)$，则$\begin{cases}y_1 = kx_1\\y_2 = kx_2\end{cases}$，两式作差，得$y_1 - y_2 = k(x_1 - x_2)$，则直线$y = kx$经过整点$(n(x_1 - x_2),nk(y_1 - y_2))$，$n\in Z$，所以直线$y = kx$经过无穷多个整点，
(3)正确.
(4)令直线$l$为$y=\frac{1}{3}x+\frac{1}{2}$，则直线$l$不过整点，
(4)错误.
(5)令直线$l$为$y = \sqrt{2}x$，则它只经过点$(0,0)$一个整点，
(5)正确. 本题正确结果为
(1)
(3)
(5)，可以任选 2 个. 

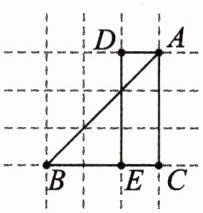
2. [2022·北京 171 中学高二期中]“曼哈顿几何”也叫“出租车几何”，是在 19 世纪由赫尔曼·闵可夫斯基提出来的. 如图是抽象的城市路网，其中|AB|是空间中定义的两点最短距离，但在城市路网中，我们只能走有路的地方，不能“穿墙”而过，所以在“曼哈顿几何”中，这两点最短距离用 d(A,B)表示，又称“曼哈顿距离”，且 d(A,B)=|AC|+|CB|，因此“曼哈顿两点间距离公式”：若 A(x₁,y₁),B(x₂,y₂)，则 d(A,B)=|x₂ - x₁|+|y₂ - y₁|，同时我们可以定义“曼哈顿圆”，即到定点的“曼哈顿距离”等于定长的点的轨迹，叫作“曼哈顿圆”.
(1)①点 A(3,5),B(2, - 1)，求 d(A,B)的值；
②求圆心在原点，半径为 1 的“曼哈顿单位圆”的方程.
(2)已知点 B(1,0)，直线 2x - y + 2 = 0，求点 B 到直线的“曼哈顿距离”的最小值.
(3)设三维空间 4 个点为 Aᵢ=(xᵢ,yᵢ,zᵢ),i = 1,2,3,4，且 xᵢ,yᵢ,zᵢ∈{0,1}. 设其中所有两点“曼哈顿距离”的平均值为 $\overline{d}$，求 $\overline{d}$ 的最大值，并列举最值成立时的一组坐标.

答案： 【解】
(1)①$d(A,B)=\vert3 - 2\vert+\vert5 + 1\vert = 7$. ②设“曼哈顿单位圆”上点的坐标为$(x,y)$，则$\vert x - 0\vert+\vert y - 0\vert = 1$，即$\vert x\vert+\vert y\vert = 1$.
(2)设直线$2x - y+2 = 0$上任意一点坐标为$C(x_1,2x_1 + 2)$，则$d(C,B)=\vert x_1 - 1\vert+\vert2x_1 + 2\vert$. 当$x_1\lt - 1$时，$d(C,B)=-3x_1 - 1$，此时$d(C,B)\gt2$； 当$-1\leqslant x_1\leqslant1$时，$d(C,B)=x_1 + 3$，此时$2\leqslant d(C,B)\leqslant4$； 当$x_1\gt1$时，$d(C,B)=3x_1 + 1$，此时$d(C,B)\gt4$. 综上所述，$d(C,B)$的最小值为 2，即点$B$到直线$2x - y+2 = 0$的“曼哈顿距离”的最小值为 2.
(3)如图，$A'B'C'D'-E'F'G'H'$为正方体，棱长为 1，则$A_i$对应正方体的八个顶点中的随机四个顶点. 当四个点在同一个面上时， ①例如，$A'$，$B'$，$C'$，$D'$，此时$\overline{d}=\frac{1 + 2+1 + 1+2 + 1}{6}=\frac{4}{3}$； ②例如，$A'$，$E'$，$G'$，$C'$，此时$\overline{d}=\frac{2 + 3+1 + 1+3 + 2}{6}=2$. 当四个点不在同一个平面时， ①例如，$A'$，$C'$，$H'$，$F'$，此时$\overline{d}=\frac{2 + 2+2 + 2+2 + 2}{6}=2$； ②例如，$A'$，$B'$，$E'$，$D'$，此时$\overline{d}=\frac{2 + 2+1 + 1+1 + 2}{6}=\frac{3}{2}$； ③例如，$A'$，$B'$，$E'$，$H'$，此时$\overline{d}=\frac{1 + 1+2 + 2+3 + 1}{6}=\frac{5}{3}$； ④例如，$A'$，$B'$，$E'$，$G'$，此时$\overline{d}=\frac{1 + 2+2 + 3+1 + 2}{6}=\frac{11}{6}$. 综上所述，$\overline{d}$的最大值为 2，可以取$A_1(0,0,0)$，$A_2(1,0,1)$，$A_3(1,1,0)$，$A_4(0,1,1)$.