《2025年练习生高中数学选择性必修第一册人教A版》

12. [2022·辽宁锦州渤海大学附属高级中学高二月考]对于任意空间向量$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$，下列命题正确的是（ ）
A. 若$\boldsymbol{a}\cdot\boldsymbol{b}=0$，则$\boldsymbol{a}$与$\boldsymbol{b}$中至少有一个为$\boldsymbol{0}$
B. 若$\boldsymbol{a}\perp\boldsymbol{b}$，则$\boldsymbol{a}\cdot\boldsymbol{b}=0$
C. $(\boldsymbol{a}\cdot\boldsymbol{b})\boldsymbol{c}-(\boldsymbol{c}\cdot\boldsymbol{a})\boldsymbol{b}=0$
D. 若$\boldsymbol{a}\cdot\boldsymbol{b}=0$，则$\boldsymbol{a}\perp\boldsymbol{b}$

答案： B

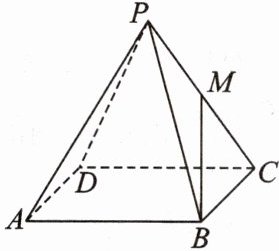
13. [2022·湖北襄阳四中高二开学考试]如图，在四棱锥 P - ABCD 中，底面 ABCD 是边长为 1 的正方形，侧棱 PA 的长为 2，且 PA 与 AB，AD 的夹角都等于$60^{\circ}$. 若 M 是 PC 的中点，则$|\overrightarrow{BM}|=$（ ）

A. $\frac{\sqrt{6}}{2}$
B. $\frac{\sqrt{6}}{3}$
C. $\frac{\sqrt{6}}{4}$
D. $\frac{\sqrt{6}}{5}$

答案： A

14. [2023·福建泉州七中高二月考]在四面体 OABC 中，棱 OA，OB，OC 两两垂直，且$OA = 1$，$OB = 2$，$OC = 3$，G 为$\triangle ABC$的重心，则$\overrightarrow{OG}\cdot(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})=$________.

答案： $\frac{14}{3}$

15. 已知点 P 为棱长等于 4 的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$内部一动点，且$|\overrightarrow{PA}| = 4$，则$\overrightarrow{PC_{1}}\cdot\overrightarrow{PD_{1}}$的值达到最小时，$\overrightarrow{PC_{1}}$与$\overrightarrow{PD_{1}}$夹角的余弦值为________.

答案： $\frac{3\sqrt{34}}{34}$

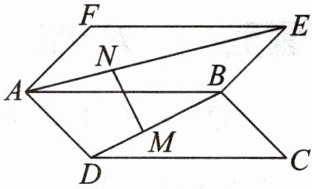
16. 如图，在矩形 ABCD 和 ABEF 中，$AB = 4$，$AD = AF = 3$，$\angle DAF=\frac{\pi}{3}$，$\overrightarrow{DM}=\lambda\overrightarrow{DB}$，$\overrightarrow{AN}=\lambda\overrightarrow{AE}$，$0＜\lambda＜1$，记$\overrightarrow{AB}=\boldsymbol{a}$，$\overrightarrow{AD}=\boldsymbol{b}$，$\overrightarrow{AF}=\boldsymbol{c}$.
（1）求异面直线 AE 与 BD 所成角的余弦值.
（2）将$\overrightarrow{MN}$用$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$表示出来，并求$|\overrightarrow{MN}|$的最小值.
（3）是否存在$\lambda$使得$MN\perp$平面 ABCD？若存在，求出$\lambda$的值；若不存在，请说明理由.

答案： （1）$\frac{1}{12}$；（2）$\overrightarrow{MN}=(1 - \lambda)\boldsymbol{a}+\lambda(\boldsymbol{c}-\boldsymbol{b})$，$|\overrightarrow{MN}|_{\min}=\sqrt{7}$；（3）存在，$\lambda=\frac{1}{2}$

17. [2021·山西晋城陵川高级实验中学校高二开学考试]设两个向量$\boldsymbol{e}_{1},\boldsymbol{e}_{2}$满足$|\boldsymbol{e}_{1}| = 2$，$|\boldsymbol{e}_{2}| = 1$，$\boldsymbol{e}_{1},\boldsymbol{e}_{2}$的夹角为$60^{\circ}$. 若向量$2t\boldsymbol{e}_{1}+7\boldsymbol{e}_{2}$与$\boldsymbol{e}_{1}+t\boldsymbol{e}_{2}$的夹角为钝角，求实数 t 的取值范围.

答案： $(-7,-\frac{\sqrt{14}}{2})\cup(-\frac{\sqrt{14}}{2},-\frac{1}{2})$

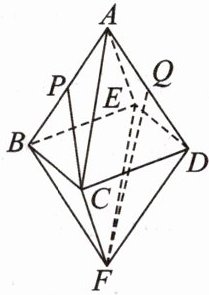
18. 正多面体也称柏拉图立体，被誉为最有规律的立体结构，是所有面都只由一种正多边形构成的多面体（各面都是全等的正多边形）. 数学家已经证明世界上只存在五种柏拉图立体，即正四面体、正六面体、正八面体、正十二面体、正二十面体. 已知一个正八面体 ABCDEF 的棱长都是 2（如图），P，Q 分别为棱 AB，AD 的中点，则$\overrightarrow{CP}\cdot\overrightarrow{FQ}=$________.

答案： 1