2025年5年高考3年模拟高中物理必修第二册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年5年高考3年模拟高中物理必修第二册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
11 (2024 重庆,7) 在万有引力作用下,太空中的某三个天体可以做相对位置不变的圆周运动,假设 $a$、$b$ 两个天体的质量均为 $M$,间距为 $2r$,其连线的中点为 $O$,另一天体 $c$(图中未画出)质量为 $m (m \ll M)$$^{[1]}$,若 $c$ 处于 $a$、$b$ 连线的垂直平分线上某特殊位置,$a$、$b$、$c$ 可视为绕 $O$ 点做角速度相同的匀速圆周运动,且相对位置不变$^{[2]}$,忽略其他天体的影响,引力常量为 $G$。则 (
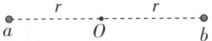
A.$c$ 的线速度大小为 $a$ 的$\sqrt{3}$倍
B.$c$ 的向心加速度大小为 $b$ 的一半
C.$c$ 在一个周期内的路程为 $2 \pi r$
D.$c$ 的角速度大小为$\sqrt{\frac{GM}{8r^3}}$
A
)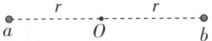
①教材回溯 研究 a、b 时,c 与 a、b 之间的万有引力可以忽略。
②关键点拨 三个天体的角速度相同,圆心在同一点。
A.$c$ 的线速度大小为 $a$ 的$\sqrt{3}$倍
B.$c$ 的向心加速度大小为 $b$ 的一半
C.$c$ 在一个周期内的路程为 $2 \pi r$
D.$c$ 的角速度大小为$\sqrt{\frac{GM}{8r^3}}$
答案:
11.A
模型建构
a、b、c绕O点做角速度相同的匀速圆周运动,构建三星模型,如图所示。

a、b、c三个天体的角速度相同,由于$m\ll M$,则对a 天体有$G\frac{MM}{(2r)^{2}}=M\omega^{2}r$,解得$\omega=\sqrt{\frac{GM}{4r^{3}}}$,D错误;设c 与a、b的连线与a、b连线中垂线的夹角为$\alpha$,对c天体有$2G\frac{Mm}{r^{2}}\cos\alpha=m\omega^{2}\frac{r}{\tan\alpha}$,解得$\alpha=30^{\circ}$,则c的轨道半径为$r_{c}=\frac{r}{\tan30^{\circ}}=\sqrt{3}r$,由$v=\omega r$,可知c的线速度大小为a的$\sqrt{3}$倍,A正确;由$a=\omega^{2}r$,可知c的向心加速度大小是b的$\sqrt{3}$倍,B错误;c在一个周期内运动的路程为$s=2\pi r_{c}=2\sqrt{3}\pi r$,C错误。
目易错警示
题设条件中明确给出天体c的质量$m$远小于天体a、b的质量$M$,言外之意就是对天体a、b的运动分析时可以不考虑天体c对天体a、b的万有引力作用,但对天体c运动分析时,其向心力来自天体a、b对天体c的万有引力的合力。
11.A
模型建构
a、b、c绕O点做角速度相同的匀速圆周运动,构建三星模型,如图所示。

a、b、c三个天体的角速度相同,由于$m\ll M$,则对a 天体有$G\frac{MM}{(2r)^{2}}=M\omega^{2}r$,解得$\omega=\sqrt{\frac{GM}{4r^{3}}}$,D错误;设c 与a、b的连线与a、b连线中垂线的夹角为$\alpha$,对c天体有$2G\frac{Mm}{r^{2}}\cos\alpha=m\omega^{2}\frac{r}{\tan\alpha}$,解得$\alpha=30^{\circ}$,则c的轨道半径为$r_{c}=\frac{r}{\tan30^{\circ}}=\sqrt{3}r$,由$v=\omega r$,可知c的线速度大小为a的$\sqrt{3}$倍,A正确;由$a=\omega^{2}r$,可知c的向心加速度大小是b的$\sqrt{3}$倍,B错误;c在一个周期内运动的路程为$s=2\pi r_{c}=2\sqrt{3}\pi r$,C错误。
目易错警示
题设条件中明确给出天体c的质量$m$远小于天体a、b的质量$M$,言外之意就是对天体a、b的运动分析时可以不考虑天体c对天体a、b的万有引力作用,但对天体c运动分析时,其向心力来自天体a、b对天体c的万有引力的合力。
12. 多选题(2024 河北,8) 2024 年 3 月 20 日,鹊桥二号中继星成功发射升空,为嫦娥六号在月球背面的探月任务提供地月间中继通讯。鹊桥二号采用周期为 $24 h$ 的环月椭圆冻结轨道(如图),近月点 $A$ 距月心约为 $2.0 × 10^3 km$,远月点 $B$ 距月心约为 $1.8 × 10^4 km$,$CD$ 为椭圆轨道的短轴,下列说法正确的是 (
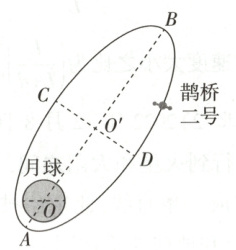
A.鹊桥二号从 $C$ 经 $B$ 到 $D$ 的运动时间为 $12 h$
B.鹊桥二号在 $A$、$B$ 两点的加速度大小之比约为 $81:1$
C.鹊桥二号在 $C$、$D$ 两点的速度方向垂直于其与月心的连线
D.鹊桥二号在地球表面附近的发射速度大于 $7.9 km/s$ 且小于 $11.2 km/s$
BD
)
A.鹊桥二号从 $C$ 经 $B$ 到 $D$ 的运动时间为 $12 h$
B.鹊桥二号在 $A$、$B$ 两点的加速度大小之比约为 $81:1$
C.鹊桥二号在 $C$、$D$ 两点的速度方向垂直于其与月心的连线
D.鹊桥二号在地球表面附近的发射速度大于 $7.9 km/s$ 且小于 $11.2 km/s$
答案:
12.BD 由开普勒第二定律知,离月球越远,鹊桥二号的速度越小,则鹊桥二号从C经B到D的运动时间应该大于12h,A错误;根据$G\frac{Mm}{r^{2}}=ma$可知$\frac{a_{A}}{a_{B}}=\frac{r_{B}^{2}}{r_{A}^{2}}$,结合题给数据得$\frac{a_{A}}{a_{B}}=\frac{81}{1}$,B正确;鹊桥二号在C、D两点的速度方向沿轨迹切线方向,不垂直于其与月心的连线,C错误;鹊桥二号在地球表面附近的发射速度大于第一宇宙速度7.9km/s且小于第二宇宙速度11.2km/s,D正确。
13. (2022 全国强基计划物理初选) 有一种关于行星带形成的传说,起源于太阳神赫利奥斯儿子法艾东被宇宙神(尤必特尔)战败。按照这个传说,一群大石块(法艾东行星应该由这些大石块形成的)太靠近木星(尤必特尔神),受到木星引力场影响,石群被瓦解成单个大石块——小行星。据估算石群的半径大约为 $10^4 km$,其质量(所有小行星质量之和)为木星质量的$\frac{1}{10^6}$。要使石群开始瓦解,它应该离木星中心的距离为(宙斯是希腊神话中最高的神,相当于罗马神话中尤必特尔——木星) (
A.$6.3 × 10^5 km$
B.$7.9 × 10^5 km$
C.$1.0 × 10^6 km$
D.$1.26 × 10^6 km$
D
)A.$6.3 × 10^5 km$
B.$7.9 × 10^5 km$
C.$1.0 × 10^6 km$
D.$1.26 × 10^6 km$
答案:
13.D设木星的质量为$M$,石群的质量为$m$,如图所示,以石群表面处的质点P为研究对象,P同时受到木星与石群对它的引力,P的加速度大小为$a_{1}=G\frac{M}{R^{2}}-G\frac{m}{r^{2}}$,而石群中心的加速度大小为$a_{2}=G\frac{M}{(R+r)^{2}}$,要使石群瓦解的条件是$a_{1}\geq a_{2}$,取等号时,表示刚好瓦解,则有$G\frac{M}{R^{2}}-G\frac{m}{r^{2}}=G\frac{M}{(R+r)^{2}}$,化简可得$M· [\frac{2r}{R}+(\frac{r}{R})^{2}]=m· \frac{1}{r^{2}}$,考虑到$r\ll R$,则$(\frac{r}{R})^{2}\approx 0$,$R+r\approx R$,可得$M· \frac{2r}{R^{3}}=m· \frac{1}{r^{2}}$,解得$R=r· \sqrt[3]{\frac{2M}{m}}=\sqrt[3]{2}× 10^{6}km\approx 1.26× 10^{6}km$,D正确,A、B、C错误。

13.D设木星的质量为$M$,石群的质量为$m$,如图所示,以石群表面处的质点P为研究对象,P同时受到木星与石群对它的引力,P的加速度大小为$a_{1}=G\frac{M}{R^{2}}-G\frac{m}{r^{2}}$,而石群中心的加速度大小为$a_{2}=G\frac{M}{(R+r)^{2}}$,要使石群瓦解的条件是$a_{1}\geq a_{2}$,取等号时,表示刚好瓦解,则有$G\frac{M}{R^{2}}-G\frac{m}{r^{2}}=G\frac{M}{(R+r)^{2}}$,化简可得$M· [\frac{2r}{R}+(\frac{r}{R})^{2}]=m· \frac{1}{r^{2}}$,考虑到$r\ll R$,则$(\frac{r}{R})^{2}\approx 0$,$R+r\approx R$,可得$M· \frac{2r}{R^{3}}=m· \frac{1}{r^{2}}$,解得$R=r· \sqrt[3]{\frac{2M}{m}}=\sqrt[3]{2}× 10^{6}km\approx 1.26× 10^{6}km$,D正确,A、B、C错误。

查看更多完整答案,请扫码查看


