《2025年5年高考3年模拟高中物理必修第二册人教版江苏专版》

1.(2024 河南南阳五校期中)一质量为$m$的物块在地球的北极与在地球赤道上的重力差为$\Delta F$,地球自转周期为$T$,则可求出地球半径$R$为 (A)

A.$\frac{\Delta F T^2}{4 \pi^2 m}$
B.$\frac{\Delta F T^2}{2 \pi^2 m}$
C.$\frac{\Delta F m T^2}{4 \pi^2}$
D.$\frac{m T^2}{4 \pi^2 \Delta F}$

答案： 1.A 关键点拨 物体在赤道处，地球的万有引力的一个分力提供物体随地球自转所需的向心力，另一分力等于物体的重力；在两极处，地球的万有引力等于物体的重力。
设物块在地球北极的重力为$mg$，在地球赤道上的重力为$mg_0$，物块在北极时，重力等于地球对其的万有引力，即$mg = \frac{GMm}{R^2}$；物块在赤道上时，由牛顿第二定律有$\frac{GMm}{R^2}-mg_0 = m\frac{4\pi^2}{T^2}R$，根据题意有$mg - mg_0=\Delta F$，联立解得$R = \frac{\Delta FT^2}{4\pi^2m}$，A正确。

2.(2025 广东广州第二中学期中)火箭载着宇宙探测器飞向某行星,火箭内平台上还放有测试仪器。起飞前,火箭静止在地球表面。起飞后,火箭以加速度$\frac{g}{4}$竖直向上做匀加速直线运动($g$为地面附近的重力加速度大小)。升到某一高度时,测试仪器对平台的压力刚好是起飞前压力的$\frac{1}{2}$,已知地球半径为$R$,该处离地面的高度$h$为 (B)

A.$2R$
B.$R$
C.$\frac{R}{2}$
D.$\frac{R}{4}$

答案： 2.B　设地球的质量为$M$，测试仪器的质量为$m$，取测试仪器为研究对象，起飞前，火箭静止在地球表面，可知测试仪器对平台的压力大小等于其重力$mg$；升到某一高度$h$处，由牛顿第二定律可得$\frac{1}{2}mg - mg_1 = ma = m\frac{g}{4}$，联立解得$g_1=\frac{1}{4}g$；根据万有引力等于重力，有$\frac{GMm}{R^2}=mg$，$\frac{GMm}{(R + h)^2}=mg_1$，联立解得$h = R$，故选B。

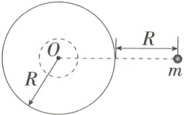
3.(2025 浙江舟山中学期中)如图所示,有一半径为$R$、质量分布均匀的球体,在距球心$2R$处有一质量为$m$的质点。若以球心$O$为中心挖去一个半径为$\frac{R}{3}$的球体,则剩余部分对该质点的万有引力变为原来的 (B)


A.$\frac{1}{27}$
B.$\frac{26}{27}$
C.$\frac{1}{8}$
D.$\frac{7}{8}$

答案：
3.B 题图解读

设球体的密度为$\rho$，则球体的质量为$M = \rho·\frac{4}{3}\pi R^3$，被挖去的小球体的质量为$M'=\rho·\frac{4}{3}\pi(\frac{R}{3})^3=\frac{1}{27}M$，可知完整球体对质点的万有引力大小为$F_1=\frac{GMm}{(2R)^2}$，被挖去的小球体对质点的万有引力大小为$F_2=\frac{GM'm}{(2R)^2}=\frac{1}{27}F_1$，则剩余部分对质点的万有引力大小为$F = F_1 - F_2=\frac{26}{27}F_1$，可知剩余部分对该质点的万有引力变为原来的$\frac{26}{27}$，B正确。
方法技巧 “填补法”的应用技巧
(1)形状的要求：大球内挖掉小球时可用，挖掉其他形状的物体时不可用此法，如挖掉的是立方体或其他不规则形状的物体，非球形物体挖掉小球等情况均不适合用此法。
(2)三心的位置关系：大球球心、小球球心、第三个球的球心（或质点），若三心共线，则三力共线，可进行代数运算；若三心不共线，则三力不共线，遵循矢量运算法则。

4.[教材 深研拓展] 如图所示,在半径为$R$、质量均匀分布的某个球体中,挖出一半径为$\frac{R}{2}$的球形空穴,空穴跟球体相切,另一均匀小球的球心位于空穴中心与空穴跟球体的切点连线所在直线上的$A$处,小球球心与球形空穴中心间的距离为$d = 2R$,引力常量为$G$,已知带空穴的球体与小球之间的万有引力大小为$F_0$。现将小球向左移动使得$d = \frac{3R}{2}$,这时球体与小球间的引力$F$与$F_0$的比值约等于 (A)


A.1.5
B.2.5
C.3.8
D.4.6

答案： 4.A 完整球体对小球的万有引力大小为$F_1 = \frac{GMm}{(2R+\frac{R}{2})^2}=\frac{4GMm}{25R^2}$，挖去部分对小球的万有引力大小为$F_2 = \frac{G\frac{1}{8}Mm}{(2R)^2}=\frac{GMm}{32R^2}$，剩余部分球体对小球的万有引力大小为$F_0 = F_1 - F_2=\frac{103GMm}{800R^2}$；当小球向左移动使$d = \frac{3}{2}R$时，完整球体对小球的万有引力大小为$F_3 = \frac{GMm}{(\frac{3R}{2})^2}=\frac{GMm}{4R^2}$，挖去部分对小球的万有引力大小为$F_4 = \frac{G\frac{1}{8}Mm}{(\frac{3}{2}R)^2}=\frac{GMm}{18R^2}$，剩余部分球体对小球的万有引力大小为$F = F_3 - F_4=\frac{7GMm}{36R^2}$，所以$\frac{F}{F_0}\approx1.5$，故选A。

5.(2025 安徽皖南八校联考)如图甲所示,质量分布均匀的球壳,对其内部任意一点的万有引力为零。将地球视为质量分布均匀的球体,从地表往地心挖一条很窄的矿井,从井口静止释放一物块。忽略一切摩擦和地球的自转,从地表到地心,物块的$a-t$图像、$v-t$图像大致正确的是 (B)

答案：
5.B 模型建构 地球对物块的引力等于半径为$(R - l)$的球体对其的引力

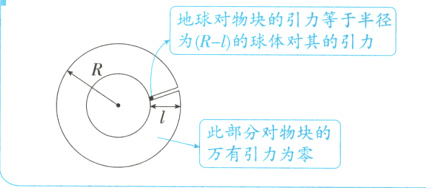
设地球的密度为$\rho$，当物块距地心的距离为$x$时，受到的万有引力为$F = \frac{GMm}{x^2}$，其中$M = \rho·\frac{4}{3}\pi x^3$，解得$F = \frac{4\pi\rho Gxm}{3}$（点拨：只有半径为$x$的那部分球体对物块有引力作用，外部球壳对物块的引力为零），根据牛顿第二定律，可得加速度为$a = \frac{F}{m}=\frac{4\pi\rho G}{3}x$，因为$x$越来越小，所以加速度$a$越来越小；$a - t$图像斜率$\frac{\Delta a}{\Delta t}=\frac{4\pi\rho G}{3}·\frac{\Delta x}{\Delta t}=\frac{4\pi\rho G}{3}v$，因物块向地心下落，速率越来越大，故$a - t$图像斜率增大，A错误，B正确；$v - t$图像的斜率是加速度，由上述分析可知，加速度越来越小，C、D错误。