2025年5年高考3年模拟高中物理必修第二册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年5年高考3年模拟高中物理必修第二册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
5.在宇宙中,单独存在的恒星占少数,更多的是双星、三星甚至多星系统。如图所示为一个简化的直线三星系统模型:三个星球的质量均为$m$,$a$、$b$ 两个星球绕处于二者连线中点的星球$c$ 做半径为$r$ 的匀速圆周运动。已知引力常量为$G$,忽略其他星体对它们的引力作用,则下列说法正确的是 (

A.星球$a$ 做匀速圆周运动的向心加速度大小为$\frac{2 G m}{r^2}$
B.星球$a$ 做匀速圆周运动的线速度大小为$\sqrt{\frac{G m}{r}}$
C.星球$b$ 做匀速圆周运动的周期为$4 \pi \sqrt{\frac{r^3}{5 G m}}$
D.若因某种原因,星球$c$ 的质量缓慢减小,则星球$a$、$b$ 的线速度均将缓慢增大
C
)
A.星球$a$ 做匀速圆周运动的向心加速度大小为$\frac{2 G m}{r^2}$
B.星球$a$ 做匀速圆周运动的线速度大小为$\sqrt{\frac{G m}{r}}$
C.星球$b$ 做匀速圆周运动的周期为$4 \pi \sqrt{\frac{r^3}{5 G m}}$
D.若因某种原因,星球$c$ 的质量缓慢减小,则星球$a$、$b$ 的线速度均将缓慢增大
答案:
5.C 对于星球$a$,星球$b$、$c$对其的万有引力的合力提供向心力,可得$\frac{Gm^2}{r^2}+G\frac{m^2}{(2r)^2}=ma_n$,故向心加速度大小为$a_n =\frac{5Gm}{4r^2}$;根据$a_n =\frac{v^2}{r}$,可得星球$a$的线速度大小为$v =\sqrt{\frac{5Gm}{4r}}$,A、B错误。根据$a_n =\frac{4\pi^2}{T^2}r$,可得星球$a$的运动周期为$T = 4\pi\sqrt{\frac{r^3}{5Gm}}$,由题意可知$a$与$b$的运行周期相同,故C正确。若因某种原因,星球$c$的质量缓慢减小,则星球$a$、$b$受到的引力将减小,会做离心运动,线速度将缓慢减小,D错误。
6.(2024 湖北武汉武昌中学月考)宇宙中存在一些离其他恒星较远的三星系统,其中有一种三星系统简化为如图所示模型,质量相等的三颗星体位于边长为$l$ 的等边三角形$ABC$ 的三个顶点上,三颗星体绕同一点做周期为$T$ 的匀速圆周运动。已知引力常量为$G$,不计其他天体对它们的影响,关于这个三星系统,下列说法中正确的是 (
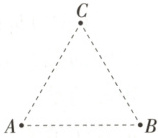
A.三颗星体做圆周运动的向心力相同
B.三颗星体的质量均为$\frac{4 \sqrt{3} \pi^2 l^3}{3 G T^2}$
C.三颗星体的自转角速度相同
D.三颗星体的线速度大小均为$\frac{2 \sqrt{3} \pi l}{3 T}$
D
)
A.三颗星体做圆周运动的向心力相同
B.三颗星体的质量均为$\frac{4 \sqrt{3} \pi^2 l^3}{3 G T^2}$
C.三颗星体的自转角速度相同
D.三颗星体的线速度大小均为$\frac{2 \sqrt{3} \pi l}{3 T}$
答案:
6.D 模型建构
三颗星体以等边三角形$ABC$的中心为圆心、沿三角形的外接圆做匀速圆周运动,轨道半径等于等边三角形外接圆的半径,如图所示。

由于向心力是矢量,三颗星体做圆周运动的向心力大小相等,方向不同,A错误;根据题意可知三颗星的质量相同,设为$M$,根据牛顿第二定律有$F_{向}=2×\frac{GM^2}{l^2}\cos 30^{\circ}=M\frac{4\pi^2}{T^2}r$,根据几何关系可知$r =\frac{\sqrt{3}}{3}l$,解得$M =\frac{4\pi^2 l^3}{3GT^2}$,故B错误;根据牛顿第二定律有$2×\frac{GM^2}{l^2}\cos 30^{\circ}=M\frac{v^2}{r}$,解得线速度大小为$v =\frac{2\sqrt{3}\pi l}{3T}$,D正确;根据公转周期可以计算公转角速度,不能计算自转角速度,C错误。
6.D 模型建构
三颗星体以等边三角形$ABC$的中心为圆心、沿三角形的外接圆做匀速圆周运动,轨道半径等于等边三角形外接圆的半径,如图所示。

由于向心力是矢量,三颗星体做圆周运动的向心力大小相等,方向不同,A错误;根据题意可知三颗星的质量相同,设为$M$,根据牛顿第二定律有$F_{向}=2×\frac{GM^2}{l^2}\cos 30^{\circ}=M\frac{4\pi^2}{T^2}r$,根据几何关系可知$r =\frac{\sqrt{3}}{3}l$,解得$M =\frac{4\pi^2 l^3}{3GT^2}$,故B错误;根据牛顿第二定律有$2×\frac{GM^2}{l^2}\cos 30^{\circ}=M\frac{v^2}{r}$,解得线速度大小为$v =\frac{2\sqrt{3}\pi l}{3T}$,D正确;根据公转周期可以计算公转角速度,不能计算自转角速度,C错误。
7.(2025 山东济南模拟)太空中存在离其他恒星系统很远、由四颗星体组成的四星系统,其他星体对它们的引力作用可忽略。稳定的四星系统有两种构成形式,其中一种是三角形,如图所示,假设三颗质量均为$m$ 的星体$A$、$B$、$C$ 分别位于等边三角形的顶点,一颗质量为$M$ 的星体$D$ 位于等边三角形的中心处,等边三角形的边长为$a$,引力常量为$G$。以星体$D$ 为参考系,下列说法正确的是 (
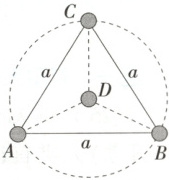
A.该稳定系统中$A$、$B$、$C$、$D$ 均做匀速圆周运动
B.$A$ 做圆周运动的半径为$\frac{\sqrt{3}}{2} a$
C.$B$ 做圆周运动的向心力大小为$\frac{\sqrt{3} G m^2}{a^2}$
D.$C$ 做圆周运动的线速度大小为$\sqrt{\frac{G(m + \sqrt{3} M)}{a}}$
D
)
A.该稳定系统中$A$、$B$、$C$、$D$ 均做匀速圆周运动
B.$A$ 做圆周运动的半径为$\frac{\sqrt{3}}{2} a$
C.$B$ 做圆周运动的向心力大小为$\frac{\sqrt{3} G m^2}{a^2}$
D.$C$ 做圆周运动的线速度大小为$\sqrt{\frac{G(m + \sqrt{3} M)}{a}}$
答案:
7.D 该稳定四星系统中,A、B、C均绕D做匀速圆周运动,A错误;A、B、C做圆周运动的向心力由各星体所受万有引力的合力提供,$F_n = 2\frac{Gm^2}{a^2}\cos 30^{\circ}+\frac{GmM}{r^2}$,$r =\frac{\sqrt{3}}{3}a$,解得$F_n =\frac{\sqrt{3}Gm(m + \sqrt{3}M)}{a^2}$,B、C错误;根据$F_n =\frac{mv^2}{r}$,解得$v =\sqrt{\frac{G(m + \sqrt{3}M)}{a}}$,D正确。
8.(2024 黑龙江佳木斯期中)宇宙中存在一些离其他恒星较远的、由质量相等的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用。设每颗星体的质量均为$m$,四颗星稳定分布在边长为$a$ 的正方形的四个顶点上,已知这四颗星均围绕正方形对角线的交点做匀速圆周运动,引力常量为$G$。则下列说法不正确的是 (
A.星体做圆周运动的轨道半径为$r = \frac{\sqrt{2}}{2} a$
B.若实验观测得到星体的半径为$R$,则星体表面的重力加速度为$g = G \frac{m}{R^2}$
C.星体做圆周运动的周期为$T = 2 \pi a \sqrt{\frac{\sqrt{2} a}{(1 + 2 \sqrt{2}) G m}}$
D.星体做圆周运动的向心力大小为$G \frac{m^2}{(\sqrt{2} a)^2}$
D
)A.星体做圆周运动的轨道半径为$r = \frac{\sqrt{2}}{2} a$
B.若实验观测得到星体的半径为$R$,则星体表面的重力加速度为$g = G \frac{m}{R^2}$
C.星体做圆周运动的周期为$T = 2 \pi a \sqrt{\frac{\sqrt{2} a}{(1 + 2 \sqrt{2}) G m}}$
D.星体做圆周运动的向心力大小为$G \frac{m^2}{(\sqrt{2} a)^2}$
答案:
8.D 模型建构
四颗星稳定分布在边长为$a$的正方形的四个顶点上,以正方形对角线的交点$O$为圆心、以顶点到对角线的交点的距离为半径做匀速圆周运动,其他三颗星体的万有引力的合力提供向心力,如图所示。
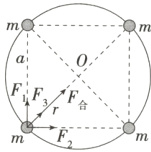
根据几何关系可得,星体做圆周运动的半径$r = a\sin 45^{\circ}=\frac{\sqrt{2}}{2}a$,故A正确。物体在星体表面所受的重力等于星体对其施加的万有引力,设物体的质量为$m_0$,则有$m_0g = G\frac{mm_0}{R^2}$,解得$g = G\frac{m}{R^2}$,故B正确。任意一颗星体都受到其他三颗星体的引力作用,根据对称性可知每颗星体所受引力的合力大小相等,且指向对角线的交点$O$,所受万有引力的合力大小为$F_{合}= G\frac{m^2}{(\sqrt{2}a)^2}+G\frac{m^2}{a^2}\cos 45^{\circ}×2 =\frac{(1 + 2\sqrt{2})Gm^2}{2a^2}$;星体做匀速圆周运动,根据牛顿第二定律有$F_{合}= m\frac{4\pi^2}{T^2}r =\frac{4\sqrt{2}\pi^2 ma}{T^2}$,联立可得$T =\sqrt{\frac{4\sqrt{2}\pi^2 a^3}{(1 + 2\sqrt{2})Gm}}= 2\pi a\sqrt{\frac{\sqrt{2}a}{(1 + 2\sqrt{2})Gm}}$,故C正确,D错误。
8.D 模型建构
四颗星稳定分布在边长为$a$的正方形的四个顶点上,以正方形对角线的交点$O$为圆心、以顶点到对角线的交点的距离为半径做匀速圆周运动,其他三颗星体的万有引力的合力提供向心力,如图所示。

根据几何关系可得,星体做圆周运动的半径$r = a\sin 45^{\circ}=\frac{\sqrt{2}}{2}a$,故A正确。物体在星体表面所受的重力等于星体对其施加的万有引力,设物体的质量为$m_0$,则有$m_0g = G\frac{mm_0}{R^2}$,解得$g = G\frac{m}{R^2}$,故B正确。任意一颗星体都受到其他三颗星体的引力作用,根据对称性可知每颗星体所受引力的合力大小相等,且指向对角线的交点$O$,所受万有引力的合力大小为$F_{合}= G\frac{m^2}{(\sqrt{2}a)^2}+G\frac{m^2}{a^2}\cos 45^{\circ}×2 =\frac{(1 + 2\sqrt{2})Gm^2}{2a^2}$;星体做匀速圆周运动,根据牛顿第二定律有$F_{合}= m\frac{4\pi^2}{T^2}r =\frac{4\sqrt{2}\pi^2 ma}{T^2}$,联立可得$T =\sqrt{\frac{4\sqrt{2}\pi^2 a^3}{(1 + 2\sqrt{2})Gm}}= 2\pi a\sqrt{\frac{\sqrt{2}a}{(1 + 2\sqrt{2})Gm}}$,故C正确,D错误。
查看更多完整答案,请扫码查看


