2025年5年高考3年模拟高中物理必修第二册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年5年高考3年模拟高中物理必修第二册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
1.(2025江苏苏州期末) 图示曲线为水平抛出的铅球的运动轨迹(不计空气阻力),关于铅球在空中的运动过程,下列说法正确的是 (
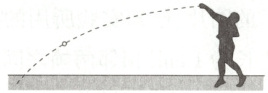
A.铅球做变加速运动
B.铅球的加速度大小和方向都不变
C.铅球的速度变化率逐渐增大
D.任意时刻加速度方向沿铅球所在位置曲线的切线方向
B
)
A.铅球做变加速运动
B.铅球的加速度大小和方向都不变
C.铅球的速度变化率逐渐增大
D.任意时刻加速度方向沿铅球所在位置曲线的切线方向
答案:
1.B 铅球水平抛出后,在空中只受重力作用,做平抛运动,属于匀变速曲线运动,则其加速度为重力加速度,大小和方向均不变,B正确,A、C错误。任意时刻的速度方向沿铅球所在位置曲线的切线方向,而其加速度方向始终竖直向下,D错误。
2.(2025北京丰台模拟) 一个人水平抛出一小球,球离开手时的初速度大小为$v_0$,落地时的速度大小为$v_t$,空气阻力忽略不计,下列哪个图像正确表示了速度矢量变化的过程 (
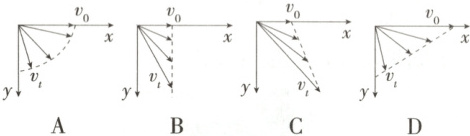
B
)
答案:
2.B 小球水平抛出后,只受到重力作用,所以水平方向上的速度不变;竖直方向上,在重力作用下速度逐渐增大,做匀加速直线运动,所以任意两个时刻的速度之差等于竖直分速度之差,为$\Delta v = g·\Delta t$,沿着竖直方向向下,B正确。
3.(2025天津英华实验学校月考) 投壶是中国古代一项兼具礼仪性与娱乐性的竞技活动。宋吕大临在《礼记传》中云:“投壶,射之细也。燕饮有射以乐宾,以习容而讲艺也”。如图所示,大人和小孩先后直立在界外同一位置,可视为在同一竖直线上不同高度处分别水平抛出“箭矢”(可视为质点),都能投入地面上的“壶内”,不计空气阻力,则 (
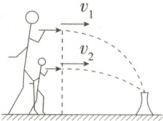
A.大人所抛出“箭矢”的速度更大
B.小孩所抛出“箭矢”的位移更大
C.大人所抛出“箭矢”的运动时间更短
D.小孩所抛出“箭矢”的运动时间更短
D
)
A.大人所抛出“箭矢”的速度更大
B.小孩所抛出“箭矢”的位移更大
C.大人所抛出“箭矢”的运动时间更短
D.小孩所抛出“箭矢”的运动时间更短
答案:
3.D 根据题意可知,抛出的“箭矢”做平抛运动,竖直方向上有$h=\frac{1}{2}gt^{2}$,解得$t = \sqrt{\frac{2h}{g}}$,由题图可知$h_{大}>h_{小}$,则有$t_{大}>t_{小}$,即小孩所抛出“箭矢”的运动时间更短,C错误,D正确;水平方向上有$x = v_{0}t$,解得$v_{0}=\frac{x}{t}=x\sqrt{\frac{g}{2h}}$,由题图可知,水平位移相等,$h_{大}>h_{小}$,则小孩所抛出“箭矢”的速度更大,A错误;抛出的“箭矢”的位移为$s = \sqrt{h^{2}+x^{2}}$,由于$h_{大}>h_{小}$,可得$s_{大}>s_{小}$(易错:位移是初位置到末位置的有向线段,包括水平和竖直分量),即大人所抛出“箭矢”的位移更大,B错误。
4.(2025北京顺义期末) 某物体做平抛运动,设该物体的瞬时速度方向与水平方向的夹角为$\theta$,$\tan \theta$ 随时间$t$变化的图像如图所示,重力加速度$g$取$10\ m/s^2$,下列说法正确的是 (
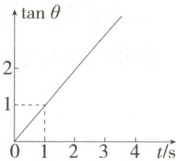
A.物体的平抛初速度的大小为$5\ m/s$
B.第$1\ s$内物体下落的高度为$10\ m$
C.第$2\ s$末物体的位移偏向角为$30°$
D.前$3\ s$内物体的速度变化量的大小为$30\ m/s$
D
)
A.物体的平抛初速度的大小为$5\ m/s$
B.第$1\ s$内物体下落的高度为$10\ m$
C.第$2\ s$末物体的位移偏向角为$30°$
D.前$3\ s$内物体的速度变化量的大小为$30\ m/s$
答案:
4.D 因$\tan\theta=\frac{v_{y}}{v_{0}}=\frac{gt}{v_{0}}$,对应图像可得$\frac{g}{v_{0}} = k$,解得$v_{0}=10\ m/s$,A错误;物体第1s内下落的高度$h_{1}=\frac{1}{2}gt_{1}^{2}=5\ m$,故B错误;0~2s内物体下落的高度为$h_{2}=\frac{1}{2}gt_{2}^{2}=20\ m$,物体的水平位移为$x_{2}=v_{0}t_{2}=20\ m$,则有$\tan\alpha=\frac{h_{2}}{x_{2}}=1$,故第2s末物体的位移偏向角为$\alpha = 45^{\circ}$,故C错误;前3s内物体的速度变化量可以看成是水平方向的速度变化量与竖直方向速度变化量的矢量和,物体做平抛运动,水平方向的速度变化量为0,所以前3s内物体的速度变化量为$\Delta v = gt_{3}=30\ m/s$,故D正确。
5.教材习题改编 如图所示,一小球从空中某点水平抛出,依次经过$A$、$B$两点。已知$A$、$B$两点间的竖直距离为$h$,小球经过$A$、$B$两点时速度方向与水平方向的夹角分别为$30°$、$45°$,不计空气阻力,重力加速度大小为$g$,则小球的初速度大小为 (
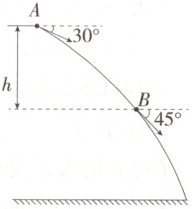
A.$\frac{\sqrt{3}gh}{3}$
B.$\sqrt{gh}$
C.$\sqrt{2gh}$
D.$\sqrt{3gh}$
D
)
A.$\frac{\sqrt{3}gh}{3}$
B.$\sqrt{gh}$
C.$\sqrt{2gh}$
D.$\sqrt{3gh}$
答案:
5.D
关键点拨
从A到B,竖直方向做加速度大小为$g$的匀加速直线运动,利用竖直分速度与水平分速度的关系,结合匀变速直线运动规律,求解小球的初速度。
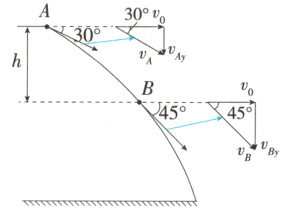
设小球的水平分速度(初速度)为$v_{0}$,则在A点的竖直分速度$v_{Ay}=v_{0}\tan30^{\circ}$,在B点的竖直分速度$v_{By}=v_{0}\tan45^{\circ}$,在竖直方向,根据匀变速直线运动规律有$v_{By}^{2}=v_{Ay}^{2}+2gh$,解得$v_{0}=\sqrt{3gh}$,D正确。
5.D
关键点拨
从A到B,竖直方向做加速度大小为$g$的匀加速直线运动,利用竖直分速度与水平分速度的关系,结合匀变速直线运动规律,求解小球的初速度。

设小球的水平分速度(初速度)为$v_{0}$,则在A点的竖直分速度$v_{Ay}=v_{0}\tan30^{\circ}$,在B点的竖直分速度$v_{By}=v_{0}\tan45^{\circ}$,在竖直方向,根据匀变速直线运动规律有$v_{By}^{2}=v_{Ay}^{2}+2gh$,解得$v_{0}=\sqrt{3gh}$,D正确。
6.(2025河南创新发展联盟联考) 如图所示,发球机在距桌面高$H$处向正前方水平射出一乒乓球(忽略空气阻力),球刚好越过网,落点到网的距离$s_{MN}=l$。已知网高为$h$,$H=3h$,重力加速度为$g$,则发球机发射该乒乓球的速度大小为 (
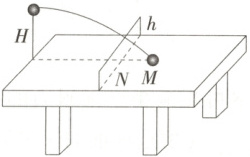
A.$\frac{(2+\sqrt{6})l}{2}\sqrt{\frac{g}{h}}$
B.$\frac{(3+\sqrt{6})l}{2}\sqrt{\frac{g}{h}}$
C.$\frac{(\sqrt{6}-2)l}{2}\sqrt{\frac{g}{h}}$
D.$\frac{(3-\sqrt{6})l}{2}\sqrt{\frac{g}{h}}$
A
)
A.$\frac{(2+\sqrt{6})l}{2}\sqrt{\frac{g}{h}}$
B.$\frac{(3+\sqrt{6})l}{2}\sqrt{\frac{g}{h}}$
C.$\frac{(\sqrt{6}-2)l}{2}\sqrt{\frac{g}{h}}$
D.$\frac{(3-\sqrt{6})l}{2}\sqrt{\frac{g}{h}}$
答案:
6.A 设乒乓球抛出点到球网的水平距离为$x$,乒乓球从发出到落到桌面过程,由平抛运动规律可得$3h=\frac{1}{2}gt_{1}^{2}$,$x + l = v_{0}t_{1}$;乒乓球从抛出点到球网的过程,有$3h - h=\frac{1}{2}gt_{2}^{2}$,$x = v_{0}t_{2}$,联立解得$v_{0}=\frac{(2 + \sqrt{6})l}{2}\sqrt{\frac{g}{h}}$,A正确。
查看更多完整答案,请扫码查看


