2025年5年高考3年模拟高中物理必修第二册人教版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年5年高考3年模拟高中物理必修第二册人教版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
4.(2025 浙江温州期中) 2025 年 7 月 15 日,搭载天舟九号货运飞船的长征七号遥十运载火箭,在我国文昌航天发射场点火发射。飞船入轨后顺利完成状态设置,成功对接于空间站天和核心舱后向端口。其运动轨迹简化如图所示:飞船从预定轨道Ⅰ的 $A$ 点第一次变轨进入椭圆轨道Ⅱ,到达椭圆轨道的远地点 $B$ 时,再次变轨进入空间站的运行轨道Ⅲ并做匀速圆周运动,与空间站实现对接。假设轨道Ⅰ和Ⅲ都近似为圆轨道,不计飞船质量的变化,地球半径为 6 400 km,地球表面的重力加速度 $g$ 为 10 m/s²,下列说法正确的是
(

A.飞船在圆轨道Ⅲ经过点 $B$ 的速度小于飞船在椭圆轨道Ⅱ经过点 $A$ 的速度
B.飞船在椭圆轨道Ⅱ经过点 $A$ 的速度可能大于 11.2 km/s
C.在轨道Ⅰ上飞船与地心连线单位时间内扫过的面积等于在轨道Ⅱ上飞船与地心连线单位时间内扫过的面积
D.飞船沿轨道Ⅲ运行的周期为 70 min
(
A
)
A.飞船在圆轨道Ⅲ经过点 $B$ 的速度小于飞船在椭圆轨道Ⅱ经过点 $A$ 的速度
B.飞船在椭圆轨道Ⅱ经过点 $A$ 的速度可能大于 11.2 km/s
C.在轨道Ⅰ上飞船与地心连线单位时间内扫过的面积等于在轨道Ⅱ上飞船与地心连线单位时间内扫过的面积
D.飞船沿轨道Ⅲ运行的周期为 70 min
答案:
4.A 由于飞船在椭圆轨道Ⅱ近地点($A$点)处的速度大于在同半径圆轨道的速度,而最终圆轨道Ⅲ的半径更大,根据$G\frac{Mm}{r^2}=m\frac{v^2}{r}$,解得$v = \sqrt{\frac{GM}{r}}$,可知线速度更小,飞船在圆轨道Ⅲ经过$B$点的速度必然小于其在椭圆轨道Ⅱ经过$A$点的速度,A正确;若飞船在椭圆轨道Ⅱ经过近地点时的速度超过$11.2 km/s$,便会脱离地球引力的束缚,不再绕地球运动,B错误;开普勒第二定律描述的是同一卫星在同一轨道与中心天体连线在相同时间内扫过的面积相等,卫星在不同的轨道上运行时,相等的时间内与中心天体连线扫过的面积不相等,C错误;近地卫星绕地球运动一周所需时间为$T_{ 近地卫星}=\frac{2\pi R}{v_1}$,$R = 6400 km$,$v_1 = 7.9 km/s$,解得$T_{ 近地卫星}\approx85 min$,根据$G\frac{Mm}{r^2}=mr(\frac{2\pi}{T})^2$,解得$T = \sqrt{\frac{4\pi^2r^3}{GM}}$,轨道Ⅲ的半径大于地球的半径,则飞船在轨道Ⅲ上的运行周期应大于$70 min$,选项D错误。
5.(2025 湖南名校联盟期末) 2025 年 看视频
4 月 24 日,我国发射神舟二十号载人飞船,如果神舟二十号飞船升空后先进入停泊轨道(即近地圆形轨道),之后进入转移轨道,最后在中国空间站轨道与天和核心舱对接,如图所示。已知中国空间站轨道为圆形轨道,距地面高度为 $h$,飞船在停泊轨道运行的周期为 $T$,地球半径为 $R$,地球表面重力加速度为 $g$,引力常量为 $G$,则下列说法正确的是
(
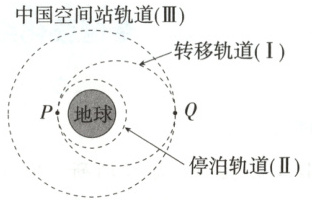
A.从停泊轨道进入转移轨道在 $P$ 点需要减速
B.天和核心舱的向心加速度大小为 $(\frac{R+h}{R})^2 g$
C.可估得地球密度为 $\frac{3\pi}{GT^2}$
D.飞船从 $P$ 点运行到 $Q$ 点需要的时间为 $T \sqrt{(1+\frac{h}{2R})^3}$
4 月 24 日,我国发射神舟二十号载人飞船,如果神舟二十号飞船升空后先进入停泊轨道(即近地圆形轨道),之后进入转移轨道,最后在中国空间站轨道与天和核心舱对接,如图所示。已知中国空间站轨道为圆形轨道,距地面高度为 $h$,飞船在停泊轨道运行的周期为 $T$,地球半径为 $R$,地球表面重力加速度为 $g$,引力常量为 $G$,则下列说法正确的是
(
C
)
A.从停泊轨道进入转移轨道在 $P$ 点需要减速
B.天和核心舱的向心加速度大小为 $(\frac{R+h}{R})^2 g$
C.可估得地球密度为 $\frac{3\pi}{GT^2}$
D.飞船从 $P$ 点运行到 $Q$ 点需要的时间为 $T \sqrt{(1+\frac{h}{2R})^3}$
答案:
5.C 飞船需要在$P$点加速,才能从停泊轨道进入转移轨道,A错误。设天和核心舱的向心加速度大小为$a$,万有引力提供向心力,有$G\frac{Mm}{(R + h)^2}=ma$;在地球表面的物体所受的万有引力等于重力,即$G\frac{Mm_0}{R^2}=m_0g$,联立解得$a = (\frac{R}{R + h})^2g$,故B错误;飞船在停泊轨道运行的周期为$T$,根据万有引力提供向心力,有$G\frac{Mm}{R^2}=m\frac{4\pi^2}{T^2}R$,解得$M = \frac{4\pi^2R^3}{GT^2}$,则地球的密度为$\rho = \frac{M}{\frac{4}{3}\pi R^3}=\frac{3\pi}{GT^2}$,故C正确;设飞船在转移轨道运行的周期为$T_2$,由开普勒第三定律有$\frac{R^3}{T^2}=\frac{(R + h_2)^3}{T_2^2}$,整理可得$T_2 = T\sqrt{(\frac{h + h_2}{2R})^3}$,故飞船在转移轨道上从$P$点飞到$Q$点所需的时间为$T_{P\to Q}=\frac{1}{2}T_2=\frac{T}{2}\sqrt{(\frac{h}{2R})^3}$,故D错误。
6.(2024 山东滨州期末) 中国自行研制、具有完全自主知识产权的“神 看视频
舟”飞船,目前已经达到或优于国际第三代载人飞船技术,其发射过程简化如下:飞船在卫星发射中心发射,由长征运载火箭送入近地点为 $A$、远地点为 $B$ 的椭圆轨道上, $A$ 点距地面的高度为 $h_1$,飞船飞行 5 圈后进行变轨,进入预定圆轨道,如图所示。设飞船在预定圆轨道上飞行 $n$ 圈所用时间为 $t$,若已知地球表面重力加速度为 $g$,地球半径为 $R$,引力常量为 $G$,不考虑地球自转。
(1) 飞船在 $B$ 点经椭圆轨道进入预定圆轨道时是加速还是减速?
(2) 求飞船在椭圆轨道上经过近地点 $A$ 时的加速度大小。
(3) 求椭圆轨道远地点 $B$ 距地面的高度 $h_2$。

舟”飞船,目前已经达到或优于国际第三代载人飞船技术,其发射过程简化如下:飞船在卫星发射中心发射,由长征运载火箭送入近地点为 $A$、远地点为 $B$ 的椭圆轨道上, $A$ 点距地面的高度为 $h_1$,飞船飞行 5 圈后进行变轨,进入预定圆轨道,如图所示。设飞船在预定圆轨道上飞行 $n$ 圈所用时间为 $t$,若已知地球表面重力加速度为 $g$,地球半径为 $R$,引力常量为 $G$,不考虑地球自转。
(1) 飞船在 $B$ 点经椭圆轨道进入预定圆轨道时是加速还是减速?
(2) 求飞船在椭圆轨道上经过近地点 $A$ 时的加速度大小。
(3) 求椭圆轨道远地点 $B$ 距地面的高度 $h_2$。

答案:
答案
(1)加速
(2)$\frac{gR^2}{(R + h_1)^2}$
(3)$\sqrt{\frac{gR^2t^2}{4\pi^2n^2}}-R$
解析
(1)飞船在$B$点经椭圆轨道进入预定圆轨道时,需要加速。
(2)不考虑地球自转,对地球表面的物体,有$m_0g = G\frac{Mm_0}{R^2}$
飞船在椭圆轨道上经过近地点$A$时,根据牛顿第二定律有$G\frac{Mm}{(R + h_1)^2}=ma_A$
联立解得飞船在椭圆轨道上经过近地点$A$时的加速度大小为$a_A = \frac{gR^2}{(R + h_1)^2}$
(3)飞船在预定圆轨道上运行时由万有引力提供向心力,有$G\frac{Mm}{(R + h_2)^2}=m\frac{4\pi^2}{T^2}(R + h_2)$
由题意可知,飞船在预定圆轨道上运行的周期$T = \frac{t}{n}$
解得$h_2 = \sqrt[3]{\frac{gR^2t^2}{4\pi^2n^2}}-R$
(1)加速
(2)$\frac{gR^2}{(R + h_1)^2}$
(3)$\sqrt{\frac{gR^2t^2}{4\pi^2n^2}}-R$
解析
(1)飞船在$B$点经椭圆轨道进入预定圆轨道时,需要加速。
(2)不考虑地球自转,对地球表面的物体,有$m_0g = G\frac{Mm_0}{R^2}$
飞船在椭圆轨道上经过近地点$A$时,根据牛顿第二定律有$G\frac{Mm}{(R + h_1)^2}=ma_A$
联立解得飞船在椭圆轨道上经过近地点$A$时的加速度大小为$a_A = \frac{gR^2}{(R + h_1)^2}$
(3)飞船在预定圆轨道上运行时由万有引力提供向心力,有$G\frac{Mm}{(R + h_2)^2}=m\frac{4\pi^2}{T^2}(R + h_2)$
由题意可知,飞船在预定圆轨道上运行的周期$T = \frac{t}{n}$
解得$h_2 = \sqrt[3]{\frac{gR^2t^2}{4\pi^2n^2}}-R$
查看更多完整答案,请扫码查看


