第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 对甲、乙两人的 5 次数学测验成绩进行统计,得出两人 5 次测验成绩数据的平均数均为 90,方差分别是 $s^2_{甲}= 51$、$s^2_{乙}= 12$. 成绩比较稳定的是
乙
(填“甲”或“乙”).
答案:
乙
2. 已知一组数据为 2,0,$-1$,3,$-4$,则这组数据的方差为
6
.
答案:
6(题目是填空题,按照要求这里应填方差的结果数值)
3. 已知一组数据 0,1,2,$x$,5 的极差是 7,则这组数据中的 $x$ 为
7或-2
.
答案:
7或-2
4. 一组数据的方差 $s^2= \frac{1}{15}[(x_1 - 10)^2 + (x_2 - 10)^2 + … + (x_n - 10)^2]$,则这组数据的平均数是
10
,$n= $15
.
答案:
平均数是$10$,$n = 15$(按照题目顺序,答案依次为$10$;$15$)
5. 甲、乙、丙三人各射击 10 次的成绩(单位:环)如图,射击成绩最稳定的是(
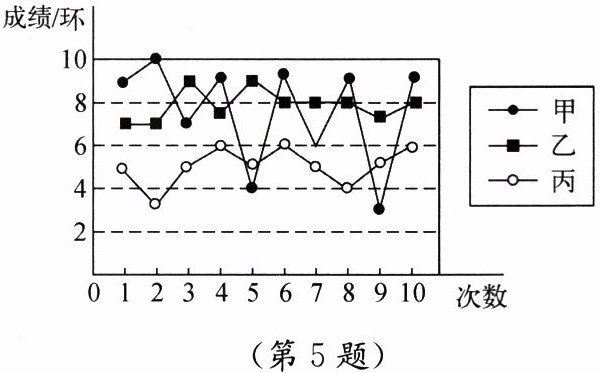
A.甲
B.乙
C.丙
D.无法判断
B
)
A.甲
B.乙
C.丙
D.无法判断
答案:
B
6. 某中学开展演讲比赛,九年级(1)班、九年级(2)班根据初赛成绩各选出 5 名选手参加复赛,两个班各选出的 5 名选手的复赛成绩(满分为 100 分)如图所示.
(1)分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析两个班级的复赛成绩.

(1)分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析两个班级的复赛成绩.

答案:
(1)九年级
(1)班复赛成绩:85,100,80,85,100
平均成绩:$\bar{x}_1=\frac{85+100+80+85+100}{5}=90$(分)
方差:$s_1^2=\frac{(85-90)^2+(100-90)^2+(80-90)^2+(85-90)^2+(100-90)^2}{5}=\frac{25+100+100+25+100}{5}=70$
九年级
(2)班复赛成绩:70,75,100,75,80
平均成绩:$\bar{x}_2=\frac{70+75+100+75+80}{5}=80$(分)
方差:$s_2^2=\frac{(70-80)^2+(75-80)^2+(100-80)^2+(75-80)^2+(80-80)^2}{5}=\frac{100+25+400+25+0}{5}=110$
(2)九年级
(1)班平均成绩高于九年级
(2)班,说明
(1)班整体成绩较好;九年级
(1)班方差小于
(2)班,说明
(1)班成绩更稳定。
(1)九年级
(1)班复赛成绩:85,100,80,85,100
平均成绩:$\bar{x}_1=\frac{85+100+80+85+100}{5}=90$(分)
方差:$s_1^2=\frac{(85-90)^2+(100-90)^2+(80-90)^2+(85-90)^2+(100-90)^2}{5}=\frac{25+100+100+25+100}{5}=70$
九年级
(2)班复赛成绩:70,75,100,75,80
平均成绩:$\bar{x}_2=\frac{70+75+100+75+80}{5}=80$(分)
方差:$s_2^2=\frac{(70-80)^2+(75-80)^2+(100-80)^2+(75-80)^2+(80-80)^2}{5}=\frac{100+25+400+25+0}{5}=110$
(2)九年级
(1)班平均成绩高于九年级
(2)班,说明
(1)班整体成绩较好;九年级
(1)班方差小于
(2)班,说明
(1)班成绩更稳定。
1. 已知一组数据 $-3$,$x$,$-2$,3,16 的中位数为 1,其方差为
46.8
.
答案:
46.8
2. 若一组数据 1,7,8,$a$,4 的平均数是 5,中位数是 $m$,极差是 $n$,则 $m + n= $
12
.
答案:
12
3. 在某中学举行的演讲比赛中,九年级 5 名参赛选手的成绩部分如下表所示,已知这 5 名选手的平均成绩为 91 分,根据表中的数据,这 5 名选手成绩的方差为(

A.2
B.6.8
C.34
D.93
B
)
A.2
B.6.8
C.34
D.93
答案:
1. 首先求$3$号选手的成绩:
设$3$号选手成绩为$x$分。
根据平均数公式$\bar{x}=\frac{x_{1} + x_{2}+\cdots+x_{n}}{n}$(这里$n = 5$,$\bar{x}=91$),可得$\frac{90 + 95+x + 89+88}{5}=91$。
化简方程:$90 + 95+x + 89+88 = 91×5$。
计算左边$90 + 95+89+88+x=(90 + 95)+(89 + 88)+x=185+177+x=362+x$,右边$91×5 = 455$。
则$362+x = 455$,解得$x = 455−362=93$。
2. 然后求方差:
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
已知$n = 5$,$\bar{x}=91$,$x_{1}=90$,$x_{2}=95$,$x_{3}=93$,$x_{4}=89$,$x_{5}=88$。
$(x_{1}-\bar{x})^{2}=(90 - 91)^{2}=(-1)^{2}=1$;$(x_{2}-\bar{x})^{2}=(95 - 91)^{2}=4^{2}=16$;$(x_{3}-\bar{x})^{2}=(93 - 91)^{2}=2^{2}=4$;$(x_{4}-\bar{x})^{2}=(89 - 91)^{2}=(-2)^{2}=4$;$(x_{5}-\bar{x})^{2}=(88 - 91)^{2}=(-3)^{2}=9$。
$s^{2}=\frac{1×(1 + 16+4 + 4+9)}{5}=\frac{34}{5}=6.8$。
所以这$5$名选手成绩的方差为$6.8$,答案是B。
设$3$号选手成绩为$x$分。
根据平均数公式$\bar{x}=\frac{x_{1} + x_{2}+\cdots+x_{n}}{n}$(这里$n = 5$,$\bar{x}=91$),可得$\frac{90 + 95+x + 89+88}{5}=91$。
化简方程:$90 + 95+x + 89+88 = 91×5$。
计算左边$90 + 95+89+88+x=(90 + 95)+(89 + 88)+x=185+177+x=362+x$,右边$91×5 = 455$。
则$362+x = 455$,解得$x = 455−362=93$。
2. 然后求方差:
根据方差公式$s^{2}=\frac{1}{n}[(x_{1}-\bar{x})^{2}+(x_{2}-\bar{x})^{2}+\cdots+(x_{n}-\bar{x})^{2}]$。
已知$n = 5$,$\bar{x}=91$,$x_{1}=90$,$x_{2}=95$,$x_{3}=93$,$x_{4}=89$,$x_{5}=88$。
$(x_{1}-\bar{x})^{2}=(90 - 91)^{2}=(-1)^{2}=1$;$(x_{2}-\bar{x})^{2}=(95 - 91)^{2}=4^{2}=16$;$(x_{3}-\bar{x})^{2}=(93 - 91)^{2}=2^{2}=4$;$(x_{4}-\bar{x})^{2}=(89 - 91)^{2}=(-2)^{2}=4$;$(x_{5}-\bar{x})^{2}=(88 - 91)^{2}=(-3)^{2}=9$。
$s^{2}=\frac{1×(1 + 16+4 + 4+9)}{5}=\frac{34}{5}=6.8$。
所以这$5$名选手成绩的方差为$6.8$,答案是B。
查看更多完整答案,请扫码查看


