《2025年伴你学九年级数学上册苏科版》

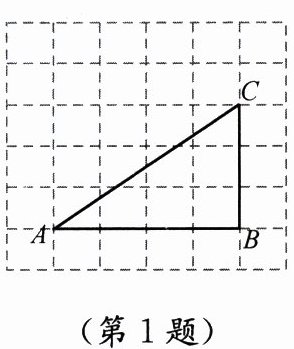
1. 如图,$ \triangle ABC $ 在每个小正方形的边长都为 1 的网格中,点 $ A $、$ B $、$ C $ 均落在格点上,用一个圆形纸片覆盖 $ \triangle ABC $,能够完全覆盖这个三角形的最小圆形纸片的半径是5/2.

答案： 5/2

2. 直角三角形的两条边的长分别为 $ 5 cm $ 和 $ 12 cm $,它的外接圆半径为6cm或6.5cm.

答案： 6cm或6.5cm

3. 根据下列已知条件,不能确定一个圆的是(C)
A.圆心与半径
B.直径
C.平面上的三个已知点
D.三角形的三个顶点

答案： C

4. 如图,方格纸上每个小正方形的边长均为 1 个单位长度,点 $ O $、$ A $、$ B $、$ C $ 在格点上,以点 $ O $ 为原点建立平面直角坐标系.
(1) 过 $ A $、$ B $、$ C $ 三点的圆的圆心 $ M $ 的坐标为(1,-1)；
(2) 求 $ \odot M $ 的面积(结果保留 $ \pi $).
设圆心$ M(1,-1) $，点$ A(-2,-1) $，则半径$ r = MA = \sqrt{(-2 - 1)^2 + (-1 - (-1))^2} = \sqrt{(-3)^2 + 0^2} = 3 $，面积$ S = \pi r^2 = 9\pi $。

答案：
(1) (1,-1)
(2) 设圆心$ M(1,-1) $，点$ A(-2,-1) $，则半径$ r = MA = \sqrt{(-2 - 1)^2 + (-1 - (-1))^2} = \sqrt{(-3)^2 + 0^2} = 3 $，面积$ S = \pi r^2 = 9\pi $。

1. 如图,一只猫发现一只老鼠溜进了鼠洞,该鼠洞只有三个出口 $ A $、$ B $、$ C $,要想同时顾及这三个出口以防老鼠出洞,这只猫最好蹲守在(D)

A.$ \triangle ABC $ 的三边高线的交点处
B.$ \triangle ABC $ 的三条角平分线的交点处
C.$ \triangle ABC $ 的三边中线的交点处
D.$ \triangle ABC $ 的三边垂直平分线的交点处

答案： D

2. 在平面直角坐标系中,点 $ A $、$ B $、$ C $ 的坐标分别为 $ (1, -1) $、$ (-2, 5) $、$ (4, -6) $. 试判断过 $ A $、$ B $、$ C $ 三点能否确定一个圆,并说明你的理由.

答案： 设经过点$A(1, -1)$和点$B(-2, 5)$的直线方程为$y = kx + b$。
代入$A(1, -1)$，得：
$-1 = k + b \quad (1)$
代入$B(-2, 5)$，得：
$5 = -2k + b \quad (2)$
从
(1)和
(2)联立解得：
$k = -2, \quad b = 1$
所以，直线$AB$的方程为$y = -2x + 1$。
将点$C(4, -6)$的坐标代入直线$AB$的方程进行验证：
$-6 = -2 × 4 + 1$
$-6 = -8 + 1$
$-6 \neq -7$
由于上式不成立，所以点$C$不在直线$AB$上。
因为点$C$不在直线$AB$上，所以点$A$、$B$、$C$不共线。
根据确定圆的条件，不共线的三点可以确定一个圆。
所以过$A$、$B$、$C$三点能确定一个圆。

3. 如图,在 $ \triangle ABC $ 中,$ AB = AC = 10 $,$ BC = 12 $,求其外接圆的半径.

答案： 过A作AD⊥BC于D，
∵AB=AC，
∴AD垂直平分BC，D为BC中点。
BC=12，
∴BD=6。
在Rt△ABD中，AB=10，BD=6，由勾股定理得AD=√(AB²-BD²)=√(10²-6²)=8。
设外接圆半径为R，圆心O在AD上，OA=OB=R，设OD=x，则OD=AD-OA=8-R。
在Rt△OBD中，OB²=OD²+BD²，即R²=(8-R)²+6²。
展开得R²=64-16R+R²+36，化简得16R=100，解得R=25/4。
25/4