《2025年伴你学九年级数学上册苏科版》

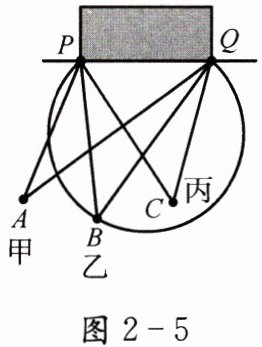
1. 如图2-5,在足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到点A时,同样乙已经助攻冲到点B,丙助攻到点C。有三种射门方式：第一种是甲直接射门；第二种是甲将球传给乙,由乙射门；第三种是甲将球传给丙,由丙射门。仅从射门角度大小考虑,应选择第第三种种射门方式。
]

答案： 第三种

2. 如图2-6,AB为⊙O的直径,∠BOC、∠BAC分别是⌢BC所对的圆心角、圆周角,直接写出图2-6①、图2-6②中∠BAC的度数,并结合图2-6③写出计算过程。
]

答案： ①45°
②60°
③
∵∠BOC是⌢BC所对的圆心角，∠BAC是⌢BC所对的圆周角，
∴∠BAC=1/2∠BOC=1/2n°

1. 如图2-7,点B、C在⊙O上。
⌢BC所对的圆心角有1个,⌢BC所对的圆周角有无数个。
]

答案： 1；无数

2. 在⊙O中画出⌢BC所对的圆心角和圆周角。所画的圆周角与圆心O有哪几种不同的位置关系？请分别画出对应的图形。
3. 根据第2题所画的不同位置关系,你能探索出同弧所对的圆周角和圆心角的数量关系吗？

答案： 2.
图1（圆心在圆周角内部）：
画⊙O，标出弧BC。
圆心角：∠BOC（顶点O，边B、C）。
圆周角：∠BAC（顶点A在⊙O上，边B、C）。
图2（圆心在圆周角一侧）：
画⊙O，标出弧BC。
圆心角：∠BOC。
圆周角：∠BAC（顶点A在⊙O上，OA与OB重合时为一种情况，此时圆周角一侧边与圆心角一边重合）。
图3（圆心在圆周角外部）：
画⊙O，标出弧BC。
圆心角：∠BOC。
圆周角：∠BAC（顶点A在⊙O上，O在∠BAC外部）。
（实际作图应使用圆规和量角器规范画出，此处为文字描述）。
3.
根据所画图形，同弧BC所对的圆周角∠BAC与圆心角∠BOC的数量关系为：
$∠BAC = \frac{1}{2}∠BOC$。