《2025年伴你学九年级数学上册苏科版》

1. 抛掷两枚质地均匀的骰子,可能出现的结果有36种.

答案： 36

2. 从-2,-1,0,1,2这5个数中任取1个数,作为关于x的一元二次方程$x^{2}-x+k= 0$的k值,则所得的方程恰好有两个不相等的实数根的概率为$\frac{3}{5}$.

答案： $\frac{3}{5}$（或 0.6对应的分数形式，根据题目要求若需要填分数形式则为$\frac{3}{5}$，若题目可接受小数则0.6也可，此处按照分数处理）由于要求不是选择题而是填空形式，直接给出数值或分数形式，故答案填写$\frac{3}{5}$。

3. 3名运动员参加定点投篮比赛,原定出场顺序是：甲第一个出场,乙第二个出场,丙第三个出场.由于某种原因,要求这3名运动员用抽签方式重新确定出场顺序,则抽签后每个运动员的出场顺序都发生变化的概率为1/3.

答案： 1/3

1. 一只不透明的袋子里装有5个除颜色外其余都相同的球,其中3个红球,2个白球.
(1)从袋中任意摸出1个球是红球的概率为$\frac{3}{5}$；

答案： $\frac{3}{5}$

(2)从袋中摸出1个球记下颜色后放回,搅匀后再摸出1个球记下颜色,求摸到1个红球和1个白球的概率.

答案： 设袋中有红球$m$个，白球$n$个（根据题意，此处我们不需要知道$m$和$n$的具体值，但理解其存在）。
由于每次摸球后都放回，所以每次摸球的概率都是独立的。
摸到红球的概率为：
$P(红球) = \frac{m}{m+n}$
摸到白球的概率为：
$P(白球) = \frac{n}{m+n}$
摸到1个红球和1个白球的情况有两种：先摸到红球再摸到白球，或者先摸到白球再摸到红球。
这两种情况是互斥的，所以摸到1个红球和1个白球的总概率为：
$P(1红1白) = P(先红后白) + P(先白后红)$
$= \frac{m}{m+n} × \frac{n}{m+n} + \frac{n}{m+n} × \frac{m}{m+n}$
$= \frac{2mn}{(m+n)^2}$
故摸到1个红球和1个白球的概率为$\frac{2mn}{(m+n)^2}$。

2. 甲、乙、丙3人同时参加“石头、剪刀、布”的游戏,3人出的手势相同的概率是多少？3人出的手势都不相同的概率是多少？

答案： 解：
1. 总可能结果数：每人有3种手势（石头、剪刀、布），3人独立出拳，总结果数为$3×3×3=27$种，且每种结果等可能。
2. 3人手势相同的概率：
3人手势相同的情况有：(石头,石头,石头)、(剪刀,剪刀,剪刀)、(布,布,布)，共3种结果。
概率为$\frac{3}{27}=\frac{1}{9}$。
3. 3人手势都不相同的概率：
3人手势都不相同，即3人分别出石头、剪刀、布，顺序不同。甲有3种选择，乙有2种（与甲不同），丙有1种（与甲、乙不同），共$3×2×1=6$种结果。
概率为$\frac{6}{27}=\frac{2}{9}$。
结论：3人手势相同的概率为$\frac{1}{9}$，都不相同的概率为$\frac{2}{9}$。

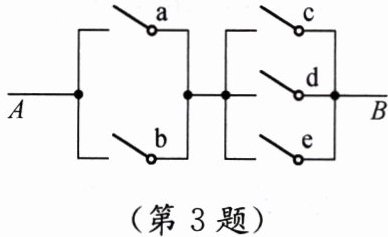
3. 如图,电路AB由a、b、c、d、e五个开关控制,现要闭合其中任意两个开关,求电路形成通路的概率.

答案： 解：
1. 基本事件总数：从5个开关中闭合2个，组合数为 $ C_{5}^{2}=\frac{5×4}{2×1}=10 $ 种。
2. 电路通路条件：假设电路结构为“a、b并联”与“c、d、e并联”串联，需两并联部分均通路，即闭合的2个开关中“1个来自a、b，1个来自c、d、e”。
3. 通路事件数：左边（a、b）选1个，右边（c、d、e）选1个，组合数为 $ C_{2}^{1}× C_{3}^{1}=2×3=6 $ 种。
4. 概率计算：通路概率 $ P=\frac{通路事件数}{基本事件总数}=\frac{6}{10}=\frac{3}{5} $。
结论：电路形成通路的概率为 $ \frac{3}{5} $。
$\boxed{\frac{3}{5}}$