第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
活动一:归纳总结
回顾本章学习中所体现的数学思想方法,并在今后的学习中有意识地运用.
(1)圆既是中心对称图形,又是轴对称图形.利用轴对称的性质得到:
(2)在探索圆心角与圆周角之间的数量关系的过程中,对圆周角相对于圆心的位置进行分类,其研究的顺序是:从
(3)在探索圆锥的侧面积计算公式的过程中,充分体现了转化思想:把圆锥侧面通过展开转化为
活动二:典型例题
回顾本章学习中所体现的数学思想方法,并在今后的学习中有意识地运用.
(1)圆既是中心对称图形,又是轴对称图形.利用轴对称的性质得到:
垂直于弦的直径平分弦,并且平分弦所对的两条弧
;利用圆绕圆心旋转任意角度
都能与原来的图形重合
的性质,得到圆心角、弧、弦之间的关系.(2)在探索圆心角与圆周角之间的数量关系的过程中,对圆周角相对于圆心的位置进行分类,其研究的顺序是:从
特殊位置(或圆心在圆周角的一边上)
入手,发展到一般,而解决一般的问题,又要用到特殊的结论.(3)在探索圆锥的侧面积计算公式的过程中,充分体现了转化思想:把圆锥侧面通过展开转化为
扇形
加以研究.活动二:典型例题
答案:
(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;任意角度;重合
(2)特殊位置(或圆心在圆周角的一边上)
(3)扇形
(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;任意角度;重合
(2)特殊位置(或圆心在圆周角的一边上)
(3)扇形
1.按照《数学实验手册(九年级全一册)》实验14的内容,将附录中的圆形纸片分别在直线上滚动、在圆上滚动、在折线上滚动,观察圆心的运动路径,与同学交流求圆心运动路径长的方法.
答案:
1. 直线上滚动:
路径:平行于直线的线段
路径长:等于直线段长度,设直线段长为$L$,路径长$=L$
2. 圆上滚动(圆形纸片半径为$r$,固定圆半径为$R$):
外滚动(沿固定圆外侧):
路径:以固定圆圆心为圆心,半径为$R+r$的圆
路径长:$2\pi(R+r)$
内滚动(沿固定圆内侧,$R>r$):
路径:以固定圆圆心为圆心,半径为$R-r$的圆
路径长:$2\pi(R-r)$
3. 折线上滚动(折线由线段$AB$、$BC$组成,内角为$\alpha$,圆半径为$r$):
路径:线段$AB$对应平行线段 + 圆弧 + 线段$BC$对应平行线段
路径长:$AB + BC + \frac{(180^\circ-\alpha)\pi r}{180^\circ}$(其中$180^\circ-\alpha$为圆弧圆心角)
路径:平行于直线的线段
路径长:等于直线段长度,设直线段长为$L$,路径长$=L$
2. 圆上滚动(圆形纸片半径为$r$,固定圆半径为$R$):
外滚动(沿固定圆外侧):
路径:以固定圆圆心为圆心,半径为$R+r$的圆
路径长:$2\pi(R+r)$
内滚动(沿固定圆内侧,$R>r$):
路径:以固定圆圆心为圆心,半径为$R-r$的圆
路径长:$2\pi(R-r)$
3. 折线上滚动(折线由线段$AB$、$BC$组成,内角为$\alpha$,圆半径为$r$):
路径:线段$AB$对应平行线段 + 圆弧 + 线段$BC$对应平行线段
路径长:$AB + BC + \frac{(180^\circ-\alpha)\pi r}{180^\circ}$(其中$180^\circ-\alpha$为圆弧圆心角)
2.在平面直角坐标$xOy$中,直线$l_{1}过点(1,2)和(-2,-1)$,$P是直线l_{1}$上一动点.
(1)请直接写出直线$l_{1}$相应的函数表达式.
(2)如图2-31①,以点$P$为圆心,5为半径作圆.当$\odot P$与坐标轴只有3个不同的公共点时,直接写出此时点$P$的坐标.
(3)如图2-31②,直线$l_{2}相应的函数表达式是y = 2x - 1$,$Q是直线l_{2}$上一动点,且$PQ= \sqrt{2}$.当以点$Q$为圆心,$\sqrt{2}为半径的圆与直线l_{1}$相切时,求此时点$P$的坐标.
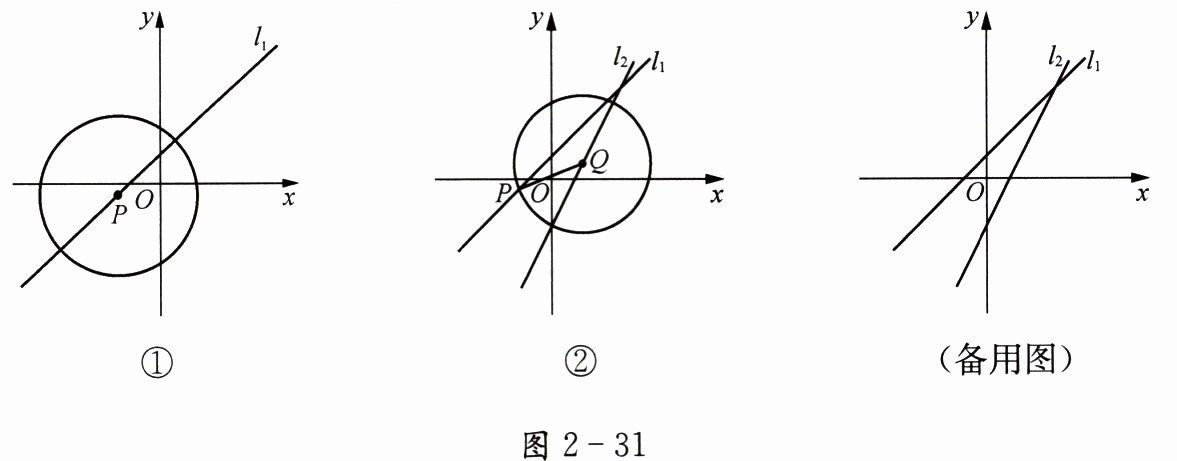
①②(备用图)
(1)请直接写出直线$l_{1}$相应的函数表达式.
(2)如图2-31①,以点$P$为圆心,5为半径作圆.当$\odot P$与坐标轴只有3个不同的公共点时,直接写出此时点$P$的坐标.
(3)如图2-31②,直线$l_{2}相应的函数表达式是y = 2x - 1$,$Q是直线l_{2}$上一动点,且$PQ= \sqrt{2}$.当以点$Q$为圆心,$\sqrt{2}为半径的圆与直线l_{1}$相切时,求此时点$P$的坐标.

①②(备用图)
答案:
(1) $y = x + 1$
(2) $(4,5)$,$(-5,-4)$,$(3,4)$,$(-4,-3)$
(3) $(-1,0)$,$(5,6)$
(1) $y = x + 1$
(2) $(4,5)$,$(-5,-4)$,$(3,4)$,$(-4,-3)$
(3) $(-1,0)$,$(5,6)$
查看更多完整答案,请扫码查看


