《2025年伴你学九年级数学上册苏科版》

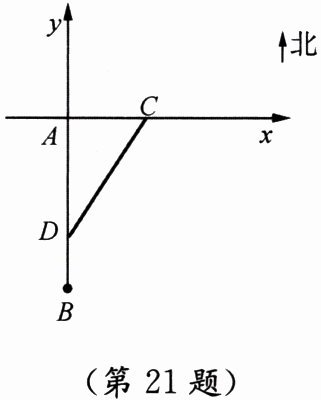
21. (10分)如图,一艘轮船以$20n mile/h$的速度由西向东航行,途中接到台风警报,台风中心正以$40n mile/h$的速度由南向北移动,距台风中心$20\sqrt{10}n mile$的圆形区域(包括边界)都属于台风区。当轮船到$A$处时,测得台风中心移到位于点$A正南方向的点B$处,且$AB = 100n mile$。若这艘轮船自点$A$处按原速度继续航行,在途中会不会遇上台风？若会,试求轮船最初遇到台风的时间；若不会,请说明理由。($1n mile\approx1852m$)

答案： 会遇上台风。
设经过 $ t $ 小时后，轮船位于点 $ C $，台风中心位于点 $ D $。
以 $ A $ 为原点，向东为 $ x $ 轴正方向，向北为 $ y $ 轴正方向建立坐标系：
轮船位置：$ C(20t, 0) $（速度 $ 20n\ mile/h $，向东航行）；
台风中心位置：$ D(0, -100 + 40t) $（$ B $ 初始坐标 $ (0, -100) $，速度 $ 40n\ mile/h $，向北移动）。
$ CD $ 距离为：
$CD = \sqrt{(20t - 0)^2 + [0 - (-100 + 40t)]^2} = \sqrt{(20t)^2 + (100 - 40t)^2}$
若相遇，则 $ CD \leq 20\sqrt{10} $，令 $ CD = 20\sqrt{10} $：
$\sqrt{(20t)^2 + (100 - 40t)^2} = 20\sqrt{10}$
两边平方得：
$(20t)^2 + (100 - 40t)^2 = (20\sqrt{10})^2$
展开化简：
$400t^2 + 10000 - 8000t + 1600t^2 = 4000$
$2000t^2 - 8000t + 6000 = 0$
$t^2 - 4t + 3 = 0$
解得 $ t_1 = 1 $，$ t_2 = 3 $。
最小正数解为 $ t = 1 $。
答：轮船最初遇到台风的时间为 $ 1 $ 小时。