《2025年伴你学九年级数学上册苏科版》

1. 甲、乙、丙 3 人随意排成一排拍照,甲恰好排在中间的概率是$\frac{1}{3}$.

答案： $\frac{1}{3}$（或对应的选择题选项字母如题目为选择题形式）

2. 从 4 根长度分别是 2 cm,3 cm,4 cm,5 cm 的小木棒中任取 3 根,能搭成三角形的概率是 (C)
A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.1

答案： C

3. 4 张扑克牌的点数分别是 2、3、4、8,将它们洗匀后背面朝上放在桌面上.
(1) 从中任意抽取 1 张,求抽到的牌的点数是偶数的概率;
(2) 从中先任意抽取 1 张,再从余下的牌中任意抽取 1 张,求抽到的两张牌的点数都是偶数的概率.

答案：
(1)
总共有$4$张牌，点数为偶数的牌有$2$，$4$，$8$共$3$张。
设“抽到的牌的点数为偶数”为事件$A$，根据概率公式$P(A)=\frac{m}{n}$（其中$n$是基本事件总数，$m$是事件$A$所包含的基本事件数），可得$P(A)=\frac{3}{4}$。
(2)
从$4$张牌中先抽一张，再从余下$3$张中抽一张的总可能情况数$n = 4×3=12$种。
要抽到的两张牌的点数都是偶数，第一次抽有$3$种可能（点数为$2$，$4$，$8$的牌），第二次抽有$2$种可能，所以抽到的两张牌的点数都是偶数的情况数$m = 3×2 = 6$种。
设“抽到的两张牌的点数都是偶数”为事件$B$，根据概率公式$P(B)=\frac{m}{n}$，可得$P(B)=\frac{6}{12}=\frac{1}{2}$。
综上，
(1)的答案是$\frac{3}{4}$；
(2)的答案是$\frac{1}{2}$。

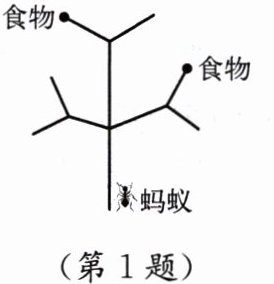
1. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都可以随机选择一条路径,并且选择每条路径的可能性相等,则它获得食物的概率是2/3.

答案： 2/3

2. 从甲、乙、丙、丁 4 名学生中选 2 名学生进行一次羽毛球单打比赛,求下列事件发生的概率.
(1) 已确定甲参加比赛,再从其余 3 名学生中任意选取 1 名,恰好选中乙;
(2) 任意选取 2 名学生,其中有乙.

答案：
(1) 已确定甲参加比赛，从乙、丙、丁3名学生中选1名，共有3种等可能结果，其中选中乙的结果有1种，所以概率为$\frac{1}{3}$。
(2) 从4名学生中任意选取2名，所有可能的结果为：(甲,乙)、(甲,丙)、(甲,丁)、(乙,丙)、(乙,丁)、(丙,丁)，共6种等可能结果。其中有乙的结果为：(甲,乙)、(乙,丙)、(乙,丁)，共3种，所以概率为$\frac{3}{6}=\frac{1}{2}$。
(1)$\frac{1}{3}$；
(2)$\frac{1}{2}$

3. 在如图的方格纸中,点 A、B、C、D、E、F 分别位于小正方形的顶点上.
(1) 从点 A、D、E、F 中任意取一点,以所取的这一点及 B、C 为顶点画三角形,则所画三角形是等腰三角形的概率是$\frac{1}{2}$;
(2) 从点 A、D、E、F 中先后任意取两个不同的点,以所取的这两点及 B、C 为顶点画四边形,求所画四边形是平行四边形的概率.$\frac{1}{3}$

答案：
(1) 从点A、D、E、F中任取一点，与B、C构成三角形，共有4种等可能情况。
取A：AB=BC，△ABC是等腰三角形；
取D：DB=DC，△DBC是等腰三角形；
取E：三边不等，不是等腰三角形；
取F：三边不等，不是等腰三角形。
等腰三角形的情况有2种，概率为$\frac{2}{4}=\frac{1}{2}$。
(2) 从A、D、E、F中先后取两个不同点，共有$4×3=12$种等可能结果（有序）。
构成平行四边形需满足对边平行且相等或对角线互相平分，符合条件的组合（无序）为{A,D}、{E,F}，对应有序结果4种：(A,D),(D,A),(E,F),(F,E)。
概率为$\frac{4}{12}=\frac{1}{3}$。
(1)$\frac{1}{2}$；
(2)$\frac{1}{3}$

4. 一项“闯关游戏”规定:在闯第 n 关时要将一枚质地均匀的骰子抛掷 n 次. 若 n 次抛掷所出现的点数之和大于 $\frac{5}{4}n^{2}$,则为过关;否则为不过关. 第二关过关的概率是 (A)
A.$\frac{13}{18}$
B.$\frac{5}{18}$
C.$\frac{1}{4}$
D.$\frac{1}{9}$

答案： A