《2025年伴你学九年级数学上册苏科版》

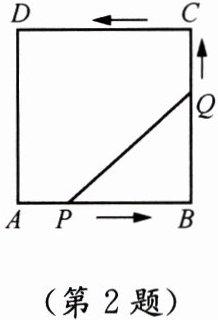
2. 如图,在边长为 6 cm 正方形 ABCD 中,点 P 从点 A 出发,沿 AB 向点 B 以 1 cm/s 的速度移动,点 Q 从点 B 出发,沿边 BC 和 CD 向点 D 以 2 cm/s 的速度移动,点 P、Q 分别从点 A、B 同时出发,当其中一点到终点时,另一点也随之停止运动。过了2，$\frac{10}{3}$s 后,$\triangle PBQ$的面积等于 $8 cm^2$。

答案： 2，$\frac{10}{3}$

3. 如图,小岛 A 在码头 B 的正西方向,A、B 相距 40 n mile。上午 9 时,一渔船和一游艇同时出发,渔船以 20 n mile/h 的速度从码头 B 向正北方向出海作业,游艇以 25 n mile/h 的速度从岛 A 返回码头 B。一段时间后,渔船因故障停航在 C 处并发出信号。游艇在 D 处收到信号后直接向渔船驶去,上午 11 时到达 C 处。游艇是在上午何时收到信号的？(1 n mile ≈ 1.852 km)

答案： 上午10时。

如图,在 $Rt\triangle ABC$ 中,$\angle B = 90^{\circ}$,AB = 6 cm,BC = 8 cm,点 P 从点 A 出发沿 AB 向点 B 以 1 cm/s 的速度移动,与此同时,点 Q 从点 B 出发沿 BC 向点 C 以 2 cm/s 的速度移动。如果点 P、Q 分别从点 A、B 同时出发,当点 Q 运动到点 C 时,两点停止运动。
1. 经过多长时间,$\triangle PBQ$ 的面积等于 $8 cm^2$？

2. $\triangle PBQ$ 的面积会等于 $10 cm^2$吗？若会,请求出此时的运动时间。

答案： 1. 解：设经过$t$秒，$\triangle PBQ$的面积等于$8cm^2$。
已知$AP = t cm$，则$PB=(6 - t)cm$，$BQ = 2t cm$。
根据三角形面积公式$S=\frac{1}{2}ah$（这里$a = PB$，$h = BQ$），可得$\frac{1}{2}(6 - t)×2t=8$。
化简得$(6 - t)t = 8$，即$6t-t^{2}=8$，移项化为标准一元二次方程形式$t^{2}-6t + 8 = 0$。
因式分解得$(t - 2)(t - 4)=0$，则$t - 2 = 0$或$t - 4 = 0$。
解得$t_{1}=2$，$t_{2}=4$。
因为$0\leqslant t\leqslant4$（点$Q$从$B$到$C$运动时间$t=\frac{8}{2}=4s$），所以经过$2s$或$4s$，$\triangle PBQ$的面积等于$8cm^2$。
2. 解：假设$\triangle PBQ$的面积等于$10cm^2$，设运动时间为$t$秒。
同样根据面积公式$\frac{1}{2}(6 - t)×2t = 10$，化简得$(6 - t)t = 10$，即$t^{2}-6t + 10 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0$（这里$a = 1$，$b=-6$，$c = 10$），判别式$\Delta=b^{2}-4ac=(-6)^{2}-4×1×10=36 - 40=-4\lt0$。
所以此方程无实数根，即$\triangle PBQ$的面积不会等于$10cm^2$。