《2025年伴你学九年级数学上册苏科版》

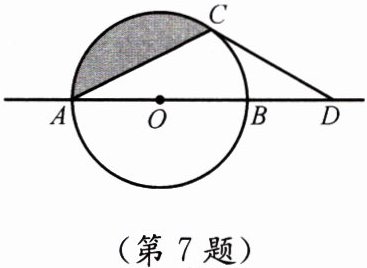
7.如图,$\odot O$半径为1,$AB是\odot O$的直径,$C是\odot O$上一点,连接$AC$,$\odot O外的一点D在直线AB$上.
(1)已知$AC = \sqrt{3}$,$OB = BD$.
①求证:$CD是\odot O$的切线;
②阴影部分的面积是______π/3.(结果保留$\pi$)
(2)当点$C在\odot O$上运动时,若$CD是\odot O$的切线,探究$\angle CDO与\angle OAC$的数量关系.∠CDO=90°-2∠OAC
(第7题)

答案：
(1)①证明：
连接OC，BC。
∵AB是⊙O直径，
∴∠ACB=90°（直径所对圆周角是直角）。
在Rt△ACB中，AB=2（半径为1，直径AB=2），AC=√3，
∴BC=√(AB²-AC²)=√(2²-(√3)²)=1。
∵OB=OC=1（⊙O半径），BC=1，
∴OB=OC=BC，△OBC是等边三角形，∠COB=60°。
∵OB=BD，OB=1，
∴BD=1，OD=OB+BD=2。
在△OCD中，OC=1，OD=2，∠COD=60°，
∴CD²=OC²+OD²-2·OC·OD·cos∠COD=1²+2²-2×1×2×cos60°=1+4-2=3，
∴OC²+CD²=1+3=4=OD²，△OCD是直角三角形，∠OCD=90°，即OC⊥CD。
∵OC是⊙O半径，
∴CD是⊙O的切线。
②π/3
(2)∠CDO=90°-2∠OAC。

1.如图,点$A$、$B$、$C$、$D是一个外角为40^{\circ}$的正多边形的顶点,若$O$为正多边形的中心,则$\angle OAD$的度数为30°.
(第1题)(第2题)

答案： 30°

2.如图,$\odot M$的半径为2,圆心$M的坐标为(3,4)$,$P是\odot M$上的任意一点,$PA\perp PB$,且$PA$、$PB与x轴分别交于A$、$B$两点,若点$A$、点$B关于原点O$对称,则$AB$的最小值为______6.

答案： 6

3.如图,在$Rt\triangle ABC$中,$\angle BCA = 90^{\circ}$,$\angle BAC的平分线交\triangle ABC外接圆于点D$,连接$BD$,已知$AB = 2AC = 4$.
(1)求$BD$的长;
(2)设点$P在\overset{\frown}{CAB}上由点C向点B$移动,但不与点$C$、$B$重合,记$\angle PBC的平分线与PD的交点为I$,求点$I随点P的移动所经过的路径长l$的取值范围.
(第3题)

答案：
(1) 在$Rt\triangle ABC$中，$\angle BCA=90^\circ$，$AB=4$，$AC=2$，则$BC=\sqrt{AB^2-AC^2}=\sqrt{16-4}=2\sqrt{3}$。$\angle BAC=60^\circ$，$AD$平分$\angle BAC$，则$\angle BAD=30^\circ$。
$AB$为外接圆直径，$\angle ADB=90^\circ$（直径所对圆周角）。在$Rt\triangle ABD$中，$BD=AB\cdot\sin\angle BAD=4\cdot\sin30^\circ=2$。
(2) 由
(1)知$AB=4$，外接圆半径为$2$，圆心$O$为$AB$中点。$CD$为直径（$CD=4$），$BD\perp BC$（直径所对圆周角为直角）。
点$I$为$\angle PBC$平分线与$PD$交点，可证$I$在以$B$为圆心，$2\sqrt{2}$为半径的圆上。轨迹为圆心角$90^\circ$的圆弧。
弧长$l=\frac{90^\circ}{360^\circ}×2\pi×2\sqrt{2}=\sqrt{2}\pi$。
(1) $BD=2$；
(2) $l=\sqrt{2}\pi$
答案
(1) $\boxed{2}$
(2) $\boxed{\sqrt{2}\pi}$