《2025年伴你学九年级数学上册苏科版》

2. ⊙O的直径为6cm,当OP= 3cm时,点P在⊙O上;当OP≤3cm时,点P不在⊙O外.

答案： ⊙O上；≤3cm

3. 已知⊙O的圆心与坐标原点重合,半径为r.若点A(2,0)在⊙O内,点P(2,2)在⊙O外,则r的取值范围是$2 ＜ r＜ 2\sqrt{2}$.

答案： $2 ＜ r＜ 2\sqrt{2}$（写实际范围，不写选项）。

4. 在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法中,不正确的是(A)
A.当a＜5时,点B在⊙A内
B.当1＜a＜5时,点B在⊙A内
C.当a＜1时,点B在⊙A外
D.当a＞5时,点B在⊙A外

答案： A

5. 设MN= 2cm.画图说明具有下列性质的点的集合是怎样的图形.
(1) 到点M的距离等于1.5cm的点的集合;
(2) 到点N的距离等于1.5cm的点的集合;
(3) 到点M的距离小于1.5cm,而到点N的距离大于1.5cm的点的集合(用阴影表示);
(4) 在所画的图形中,你还能再提出一个关于点的集合的问题吗?

答案：
(1)到点$M$的距离等于$1.5cm$的点的集合：
以点$M$为圆心，$1.5cm$为半径画圆，该圆即为所求的点的集合。
(2)到点$N$的距离等于$1.5cm$的点的集合：
以点$N$为圆心，$1.5cm$为半径画圆，该圆即为所求的点的集合。
(3) 分别以M，N为圆心，以$1.5cm$，$1.5cm$为半径画圆（圆M与圆N）。
在圆N内部（不包括圆N本身）且在圆M外部（不包括圆M本身）的区域打上阴影，该阴影区域即为所求的点的集合。
(4)问题：到点$M$和点$N$的距离都等于或小于$1cm$的点的集合是怎样的图形（答案不唯一）。

1. 已知AB为⊙O的直径,P为⊙O上任意一点(不与点A、B重合),则点P关于AB的对称点P′与⊙O的位置关系为(C)
A.在⊙O内
B.在⊙O外
C.在⊙O上
D.不能确定

答案： C

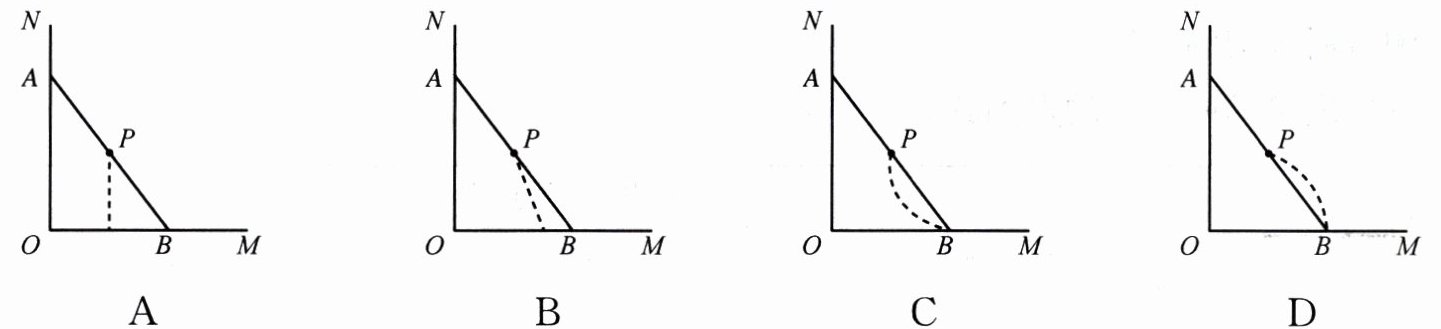
2. 木杆AB斜靠在墙壁上,当木杆的顶端A沿墙壁NO竖直下滑时,木杆的底端B也随之沿地面OM水平向右滑动.下图中虚线表示木杆的中点P变化的轨迹,其中正确的是(D)

答案： D

3. 在矩形ABCD中,AB= 6,AD= 8.若作⊙A,使B,C,D三点至少有一点在⊙A内,至少有一点在⊙A外,则⊙A的半径r的取值范围是6＜ r ＜ 10.

答案： $6＜ r ＜ 10$（以题目要求的形式填写答案则为具体数值范围，不以选择形式呈现）。

4. 如图,在某海域中,以点A为圆心、3km为半径的圆形区域为暗礁区.救援船要从点B处前往点A处,A、B两点之间的距离是10km,如果救援船始终保持10km/h的速度行驶,那么在什么时段内,救援船是安全的? 救援船何时进入暗礁区域?

答案： 1. 首先计算救援船从$B$到$C$的时间：
已知$AB = 10km$，$AC = 3km$，则$BC=AB - AC$。
根据公式$t=\frac{s}{v}$（其中$t$为时间，$s$为路程，$v$为速度），$v = 10km/h$。
$BC$的距离$s_{BC}=10 - 3=7km$。
那么救援船从$B$到$C$的时间$t_{1}=\frac{s_{BC}}{v}=\frac{7}{10}=0.7h$。
救援船从$B$到$A$的时间$t_{2}=\frac{AB}{v}=\frac{10}{10}=1h$。
2. 然后分析安全时段和进入暗礁时间：
救援船在$0$到$0.7h$这个时段内是安全的（因为在$0$到$0.7h$时，救援船还未到达暗礁区边界$C$点）。
救援船在$0.7h$时进入暗礁区域（当行驶时间为$t = 0.7h$时，刚好到达暗礁区边界$C$点）。
答：在$0$到$0.7h$时段内救援船是安全的，救援船在$0.7h$时进入暗礁区域。