第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 将以下四个图形折叠得到的立体图形依次是(
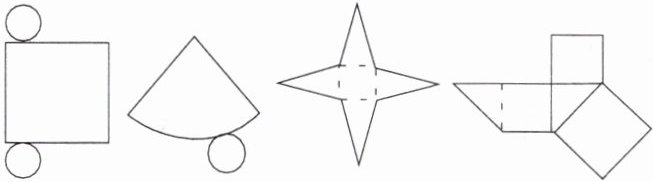
A.圆锥、圆柱、四棱柱、三棱柱
B.圆柱、圆锥、三棱锥、三棱柱
C.圆柱、圆锥、四棱锥、三棱柱
D.圆锥、圆柱、四棱柱、三棱锥
C
)
A.圆锥、圆柱、四棱柱、三棱柱
B.圆柱、圆锥、三棱锥、三棱柱
C.圆柱、圆锥、四棱锥、三棱柱
D.圆锥、圆柱、四棱柱、三棱锥
答案:
C
2. 下列图形经过折叠不能围成一个棱柱的是(
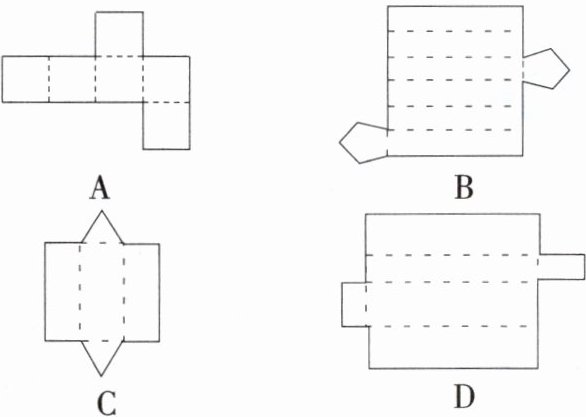
B
)
答案:
B
3. 在下图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添加方法有
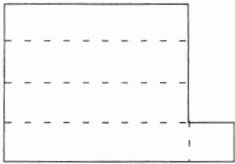
4
种.
答案:
4
4. 星期天,李静同学用纸盒制成一个底面边长均为4 cm、侧棱长为6 cm的正六棱柱形的笔筒,如图所示.
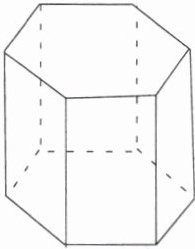
(1) 这个笔筒有多少个面?它们分别是什么形状?
(2) 这个六棱柱共有多少条棱?它们的长度分别是多少?
(3) 制作侧面共用去了多少材料?

(1) 这个笔筒有多少个面?它们分别是什么形状?
(2) 这个六棱柱共有多少条棱?它们的长度分别是多少?
(3) 制作侧面共用去了多少材料?
答案:
解:
(1)这个笔筒共有7个面,底面是正六边形、侧面都是长方形.
(2)这个六棱柱共有18条棱,底面的边长均为4 cm,侧棱长均为6 cm.
(3)制作侧面共用去的材料为4×6×6=144(cm²).
(1)这个笔筒共有7个面,底面是正六边形、侧面都是长方形.
(2)这个六棱柱共有18条棱,底面的边长均为4 cm,侧棱长均为6 cm.
(3)制作侧面共用去的材料为4×6×6=144(cm²).
1. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是(
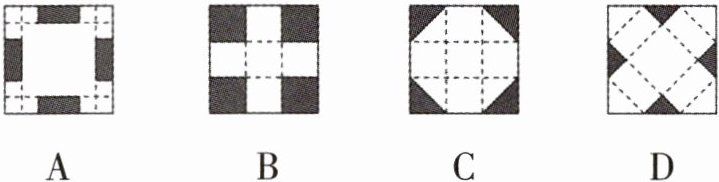
D
)
答案:
D
2. 下列图形经过折叠不能围成三棱柱的是(
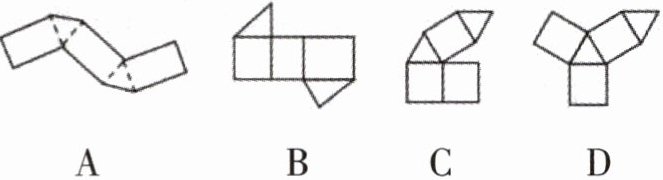
C
)
答案:
C
3. 如图,用高为6 cm,底面直径为4 cm的圆柱A的侧面展开图,再围成不同于A的另一个圆柱B,则圆柱B的体积为(
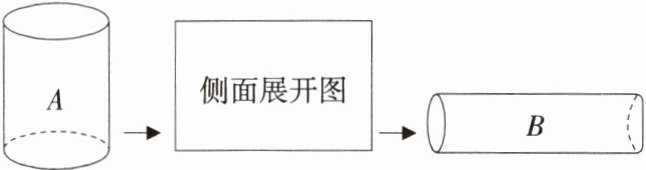
A.$24\pi \, cm^3$
B.$36\pi \, cm^3$
C.$36 \, cm^3$
D.$40 \, cm^3$
C
)
A.$24\pi \, cm^3$
B.$36\pi \, cm^3$
C.$36 \, cm^3$
D.$40 \, cm^3$
答案:
C
4. 如图是一张铁皮:
(1)计算该铁皮的面积;
(2)该铁皮能否做成一个长方体盒子(底面固定,如图)? 若能,画出它的立体图形,并计算它的体积;若不能,请说明理由.
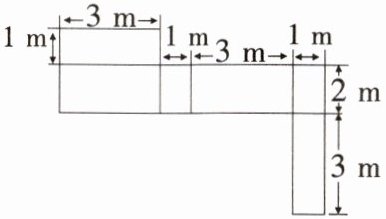
(1)计算该铁皮的面积;
(2)该铁皮能否做成一个长方体盒子(底面固定,如图)? 若能,画出它的立体图形,并计算它的体积;若不能,请说明理由.

答案:
解:
(1)该铁皮的面积为3×1×2+3×2×2+2×1×2=22(m²).
(2)该铁皮能做成一个长方体盒子,画立体图形略.
该长方体盒子的长为3 m,宽为2 m,高为1 m,所以它的体积为3×2×1=6(m³).
(1)该铁皮的面积为3×1×2+3×2×2+2×1×2=22(m²).
(2)该铁皮能做成一个长方体盒子,画立体图形略.
该长方体盒子的长为3 m,宽为2 m,高为1 m,所以它的体积为3×2×1=6(m³).
查看更多完整答案,请扫码查看


