第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
4. 有以下四种实践方式:①木匠弹墨线;②打靶瞄准;③弯曲公路改直;④拉绳插秧。其中可以用基本事实“两点确定一条直线”来解释的有
①②④
(填序号)。
答案:
①②④
5. 如图,图中有
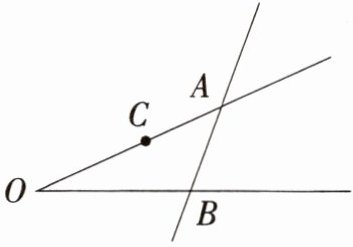
1
条直线,是直线AB
;以 $ O $ 为端点的射线有2
条,是射线OA、射线OB
;有5
条线段,是线段OC、CA、OA、OB、AB
。
答案:
1 直线AB 2 射线OA、射线OB 5 线段OC、CA、OA、OB、AB
6. 读语句画图。
(1) 连接 $ BC $,$ AD $;
(2) 画直线 $ AB $,$ CD $ 交于点 $ E $;
(3) 延长 $ BC $ 并与 $ DA $ 反向延长线相交于点 $ F $;
(4) 连接 $ AC $,$ BD $ 交于点 $ O $。
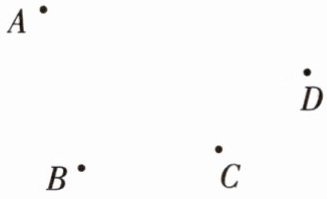
(1) 连接 $ BC $,$ AD $;
(2) 画直线 $ AB $,$ CD $ 交于点 $ E $;
(3) 延长 $ BC $ 并与 $ DA $ 反向延长线相交于点 $ F $;
(4) 连接 $ AC $,$ BD $ 交于点 $ O $。
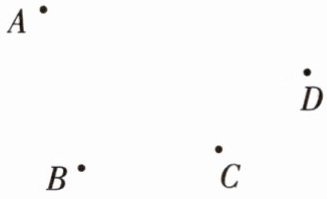
答案:
解:
解:

7. (1) 平面上有三个点,经过两点画一条直线,则可以画几条直线?
(2) 平面上有四个点,经过两点画一条直线,则可以画几条直线?
(2) 平面上有四个点,经过两点画一条直线,则可以画几条直线?
答案:
解:
(1)1条或3条.
(2)1条或4条或6条.(点的位置不确定,需分类讨论)


解:
(1)1条或3条.
(2)1条或4条或6条.(点的位置不确定,需分类讨论)


阅读下表,解答问题:
(1) 在表中空白处画出图形,并写出线段总条数 $ N $;
(2) 猜测线段总条数 $ N $ 与线段上的总数 $ n $(包括线段的两端点)有什么关系;
(3) 有一辆客车往返于 $ A $,$ B $ 两地,中途停靠 8 个站点,任意两站间的票价都不同(同一区间内的往返票价相同),假如你是客运公司经理,要定多少种不同的票价?要准备多少种不同的车票?
(1) 在表中空白处画出图形,并写出线段总条数 $ N $;
(2) 猜测线段总条数 $ N $ 与线段上的总数 $ n $(包括线段的两端点)有什么关系;
(3) 有一辆客车往返于 $ A $,$ B $ 两地,中途停靠 8 个站点,任意两站间的票价都不同(同一区间内的往返票价相同),假如你是客运公司经理,要定多少种不同的票价?要准备多少种不同的车票?
答案:
解:
(1)
线段AB上的点数n(包括A,B两点) 图例 线段总条数N
3 ACB 3=2+1
4 ACDB 6=3+2+1
5 ACDEB 10=4+3+2+1
6 ACDEFB 15=5+4+3+2+1
7 ACDEFGB 21=6+5+4+3+2+1
(2)N=1+2+3+4+…+(n−2)+(n−1)
=[1+(n−1)]×(n−1)/2=n(n−1)/2.
即线段总条数N与线段上的点数n的关系是N=n(n−1)/2.
(3)由题意可知,n=10,所以N=45,即定45种票价.又由于客车是往返行驶的,故要准备2×45=90(种)不同的车票.
(1)
线段AB上的点数n(包括A,B两点) 图例 线段总条数N
3 ACB 3=2+1
4 ACDB 6=3+2+1
5 ACDEB 10=4+3+2+1
6 ACDEFB 15=5+4+3+2+1
7 ACDEFGB 21=6+5+4+3+2+1
(2)N=1+2+3+4+…+(n−2)+(n−1)
=[1+(n−1)]×(n−1)/2=n(n−1)/2.
即线段总条数N与线段上的点数n的关系是N=n(n−1)/2.
(3)由题意可知,n=10,所以N=45,即定45种票价.又由于客车是往返行驶的,故要准备2×45=90(种)不同的车票.
查看更多完整答案,请扫码查看


