《2025年学习之友七年级数学上册北师大版》

3. 观察下面三组数：
$1$,$3$,$5$,$7$,$9$,$11$,$13$,$15…$
$2$,$5$,$8$,$11$,$14$,$17$,$20$,$23…$
$7$,$13$,$19$,$25$,$31$,$37$,$43$,$49…$
这三组数具有共同的特点.现在有具有上述特点的一组数,并知道第一个数是$3$,第三个数是$11$,则其第$n$个数为(C)
A.$8n - 5$
B.$n^{2} + 2$
C.$4n - 1$
D.$2n^{2} - 4n + 5$

答案： C

4. 观察下列各式：
① $1 = 1^{2}$；② $2 + 3 + 4 = 3^{2}$；
③ $3 + 4 + 5 + 6 + 7 = 5^{2}$；
④ $4 + 5 + 6 + 7 + 8 + 9 + 10 = 7^{2}…$
请你根据观察得到的规律判断下列各式正确的是(C)
A.$1005 + 1006 + 1007 + … + 3016 = 2011^{2}$
B.$1005 + 1006 + 1007 + … + 3017 = 2011^{2}$
C.$1006 + 1007 + 1008 + … + 3016 = 2011^{2}$
D.$1007 + 1008 + 1009 + … + 3017 = 2011^{2}$

答案： C

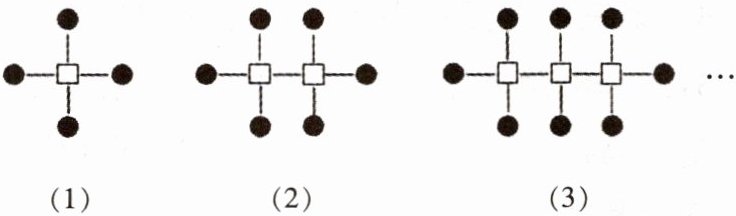
5. 下列图形是由一些小正方形和实心圆按一定规律排列而成的,按此规律排列下去,第$20$个图形中有42个实心圆.
]

答案： 42

6. 观察下面的图形(每个正方形的边长均为1)和相应的等式,探究其中的规律：

(1) 写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示；5×$\frac{5}{6}$=5-$\frac{5}{6}$(2) 猜想并写出与第n个图形对应的等式.n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$

答案： 解:
(1)5×$\frac{5}{6}$=5-$\frac{5}{6}$.(图略) （2）n×$\frac{n}{n+1}$=n-$\frac{n}{n+1}$.

如图是用棋子摆成的“上”字：

如果按照以上规律继续摆下去,那么通过观察,可以发现：
(1) 第④个、第⑤个“上”字分别需要用18和22枚棋子；
(2) 第$n$个“上”字需要用4n+2枚棋子；
(3) 七 (3) 班有$50$名同学,把每一位同学当作一枚棋子,能否让这$50$枚“棋子”按照以上规律恰好站成一个“上”字？若能,请计算最下面一“横”的学生数；若不能,请说明理由.
解:4n+2=50,n=12.最下面的一“横”上的学生数为2n+1=25.

答案： 解:
(1)18 22. （2）(4n+2). （3）4n+2=50,n=12.最下面的一“横”上的学生数为2n+1=25.