《2025年学习之友七年级数学上册北师大版》

6. 为了促使海南的水果很快运往内地,现有一批水果包装质量为每筐$25kg$,现抽取$8$筐样品进行检测,结果称重记录如下(单位：$kg$)：$27,24,23,28,21,26,22,27$。为了求得$8$筐样品的总质量：
(1)请你选择一个恰当的基准数。
(2)根据你选取的基准数,用正、负数填写下表：

(3) 这$8$筐水果的总质量是多少？

答案：

(1)基准数不唯一,如以25为基准数
(2)

(3)这8筐水果的总质量为:[2+(-1)+(-2)+3+(-4)+1+(-3)+2]+25×8=-2+200=198(kg).

7. 王先生到市行政中心大楼办事,假定乘电梯向上一楼记作$+1$,向下一楼记作$-1$,王先生从$1$楼出发,电梯上下楼层依次记录如下(单位：层)：$+6,-3,+10,-8,+12,-7,-10$。
(1) 请你通过计算说明王先生最后是否回到出发点$1$楼。
(2) 该中心大楼每层高$3m$,电梯每向上或向下$1m需要耗电0.2$度,根据王先生现在所处的位置,请你算算,他办事时电梯需要耗电多少度？

答案：
(1)(+6)+(-3)+(+10)+(-8)+(+12)+(-7)+(-10)
=0
王先生最后能回到出发点1楼.
(2)王先生走过的路程是
3×(|+6|+|-3|+|+10|+|-8|+|+12|+|-7|+|-10|)
=3×(6+3+10+8+12+7+10)
=3×56
=168m
他办事时电梯需要耗电168×0.2=33.6度.

1. 快递员骑摩托车从总部$A$点出发,在一条南北走向的街道上来回收取包裹。记录他连续行驶的情况如下(以向南为正方向,单位：千米)：$5,2,-4,-3\frac{1}{2},3,-2.5,6$。
(1)他最后一次收取包裹后在出发点$A$的什么位置？
(2)如果摩托车每千米耗油$30$毫升,出发前摩托车有油$1000$毫升,快递员在收完包裹后能回到出发点吗？

答案： $(1)5+2+(-4)+(-3\frac{1}{2})+3+(-2.5)+6$
$=(5+2+3+6)+[(-4)+(-3\frac{1}{2})+(-2.5)]$
=16+(-10)
=6(千米)
答:最后一次收取包裹后，他在出发点A的南方6千米处.
(2)|5|+|2|+|-4|+|$-3\frac{1}{2}$|+|3|+|-2.5|+|6|
=5+2+4+3.5+3+2.5+6
=26(千米)
回到出发点共耗油(26+6)×30=960(毫升),因为960＜1000,所以快递员在收完包裹后能回到出发点.

2. 如图所示,将数字$-2,-1,0,1,2,3,4,5,6,7这10$个数字分别填写在五角星中每两条线的交点处(每个交点只填写一个数),将每一行上的四个数相加为一个数,共得到$5$个数,分别设为$a_{1},a_{2},a_{3},a_{4},a_{5}$,则：

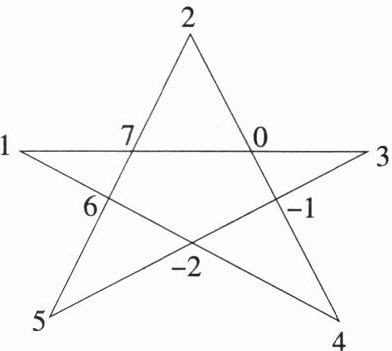
(1) 求$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$的值；
(2) 交换其中任意两个数的位置后,$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$的值是否改变？说明理由。

答案： $(1)a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=2×[(-1)+(-2)+0+1+2+3+4+5+6+7]=50.$
(2)交换其中任意两数的位置后$,a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$的值不变仍为50.这是因为,无论怎样改变位置，其中的每个数都用了两次,即$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=2[(-1)+(-2)+0+1+2+3+4+5+6+7]=2×25=50.$