《2025年学习之友七年级数学上册北师大版》

4. 代数式 $ 3x^{2}-4x + 6$ 的值为 $ 9$,则 $ x^{2}-\frac{4}{3}x + 6$ 的值为(D)
A.$18$
B.$12$
C.$9$
D.$7$

答案： D

5. 根据如图所示的计算程序,若输入的值 $ x = - 1$,则输出的 $ y= $2。
]

答案： 2

6. 已知 $ x + y = 6$,$ xy = - 3$,则 $ 3x - 2xy + 3y$ 的值为24。

答案： 24

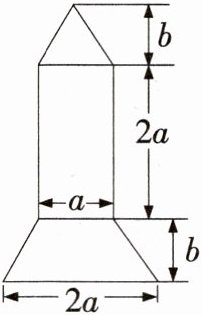
7. 重量为 $ m\ kg$ 的茶叶总售价为 $ p$ 元,设单价每千克为 $ d$ 元。
(1)试求单价 $ d$(用含字母 $ m$,$ p$ 的式子表示)；
(2)第一种 $ m = 0.25$,$ p = 15$；第二种 $ m = 0.75$,$ p = 60$,哪种茶叶便宜些？

答案： 解:
(1)$d=\frac{p}{m}$
(2)第一种$d=\frac{15}{\frac{1}{4}}=15×4=60$(元/kg);第二种$d=\frac{60}{\frac{3}{4}}=80$(元/kg).因为60＜80,所以第一种便宜.

8. 某商场销售一种西装和领带,西装每套定价 $ 500$ 元,领带每条定价 $ 100$ 元,“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案。现某客户要到商场购买西装 $ 20$ 套,领带 $ x$ 条$(x ＞ 20)$。
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的 $ 90\%$ 付款。
(1)若客户按方案一购买,需付款$(100x+8000)$元；若客户按方案二购买,需付款______$(90x+9000)$元。
(2)若 $ x = 30$,请通过计算说明此时按哪种方案购买较为合算？
(3)当 $ x = 30$ 时,你能给出一种更为省钱的购买方案吗？试写出你的购买方案,并计算此方案需要付款多少元？

答案：
(1)$(100x+8000)$元；$(90x+9000)$元
(2)当$x=30$时,方案一费用:$100x+8000=100×30+8000=11000$（元）;方案二费用:$90x+9000=90×30+9000=11700$（元）;因为$11000＜11700$,所以按方案一购买较合算;
(3)先按方案一购买20套西装获赠20条领带,再按方案二购买10条领带.$20×500+100×0.9×10=10900$(元).故此方案需要付款10900元.

一个数值转换器,原理如图所示,若开始输入的数是 $ 7$,可发现第一次输出的结果是 $ 12$,第 $ 2$ 次输出的结果是 $ 6$。

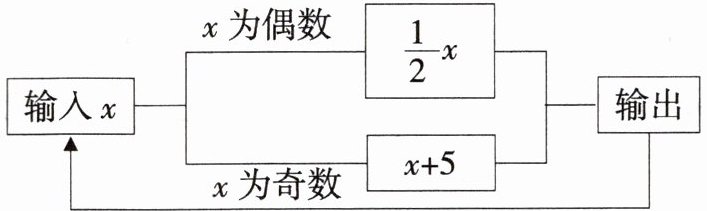
(1)第 $ 3$ 次输出的结果是3,第 $ 4$ 次输出的结果是8；
(2)你能推出第 $ 2025$ 次输出的结果吗？请说说你的方法。
能推出第2025次输出的结果是3,理由如下:第一次为12,第2次为6,第3次为3,第4次为8,第5次为4,第6次为2,第7次为1,第8次为6,归纳得出输出的结果从第二次开始以6,3,8,4,2,1循环,$(2025-1)÷6=337\cdots\cdots2$,则第2025次输出的结果是3.

答案：
(1)3；8
(2)能推出第2025次输出的结果是3,理由如下:第一次为12,第2次为6,第3次为3,第4次为8,第5次为4,第6次为2,第7次为1,第8次为6,归纳得出输出的结果从第二次开始以6,3,8,4,2,1循环,$(2025-1)÷6=337\cdots\cdots2$,则第2025次输出的结果是3.