《2025年学习之友七年级数学上册北师大版》

6. 已知 $A = 2a^2 + 3ab - 1$,$B = -a^2 + ab - 1$。
求：(1) $A + 2B$；(2) $A - 2B$。

答案：
(1)解:A+2B=(2a²+3ab-1)+2(-a²+ab-1)=2a²+3ab-1-2a²+2ab-2=5ab-3.
(2)解:A-2B=(2a²+3ab-1)-2(-a²+ab-1)=2a²+3ab-1+2a²-2ab+2=4a²+ab+1.

7. 天平的左边挂重为 $2m^2 - 3m + 3$,若右边挂重为 $m^2 - 3m + 3$,其中 $m \neq 0$,请你猜一猜：天平会倾斜吗？如果出现倾斜,将向哪边倾斜？

答案： 解:(2m²-3m+3)-(m²-3m+3)=2m²-3m+3-m²+3m-3=m².
因为m≠0,所以m²＞0,即2m²-3m+3＞m²-3m+3,因此天平向左倾斜.

8. 如图所示,化简 $|3 - x| - |x - 2| - |2x + 1|$。

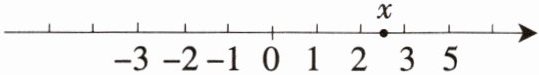
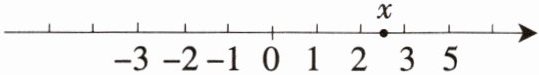
答案： 解:因为2＜x＜3,所以|3-x|=3-x,|x-2|=x-2,|2x+1|=2x+1
原式=3-x-(x-2)-(2x+1)=3-x-x+2-2x-1=-4x+4.

9. 有这样一道计算题：“计算 $(2x^3 - 5x^2y - 2xy^2) - (x^3 - 2xy^2 + y^3) + (-x^3 + 5x^2y - y^3)$ 的值,其中 $x = \frac{1}{2}$,$y = -3$”,小明把 $x = \frac{1}{2}$ 错看成 $x = -\frac{1}{2}$,但计算结果仍正确,你知道为什么吗？

答案： 解:原式=2x³-5x²y-2xy²-x³+2xy²-y³-x³+5x²y-y³=-2y³.
因为原式化简后的结果中不含有x,所以不管小明把x看成什么数,都不影响结果的正确性.

10. 在“安居工程”住房小区建设中,为了提高业主的宜居环境,某小区规划修建一个广场(平面图形如图所示)
(1) 用含 $m$,$n$ 的代数式表示该广场的面积 $S$；
(2) 若 $m$,$n$ 满足 $(m - 6)^2 + |n - 5| = 0$,求出该广场的面积。

答案：
(1)解:根据题意得:S=2m·2n-m(2n-0.5n-n)=3.5mn;
(2)因为(m-6)²+|n-5|=0,所以m=6,n=5,则S=3.5×6×5=105.

某数学老师在课外活动中做了一个有趣的游戏：首先发给 $A$,$B$,$C$ 三个同学相同数量的扑克牌(假定发到每个同学手中的扑克牌数量足够多),然后依次完成以下三个步骤：
第一步,$A$ 同学拿出两张扑克牌给 $B$ 同学；
第二步,$C$ 同学拿出三张扑克牌给 $B$ 同学；
第三步,$A$ 同学手中此时有多少张扑克牌,$B$ 同学就拿出多少张扑克牌给 $A$ 同学。
请确定最终 $B$ 同学手中剩余的扑克牌的张数。

答案： 解:设开始发给A、B、C三个同学的扑克牌都是x张,
因为B同学从A同学处拿来两张扑克牌,又从C同学处拿来三张扑克牌,
所以B同学有(x+2+3)张牌,A同学有(x-2)张牌,
所以给A同学后B同学手中剩余的扑克牌的张数为:x+2+3-(x-2)=x+5-x+2=7.