第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
3. 一个物体的外形是圆柱,但不清楚它的内部结构,现在用一组水平的平面去截这个物体,从上至下的五个截面依次如图所示,则这个物体可能是(

B
)
答案:
B
4. 用一个平面去截一个几何体,得到的截面是八边形,这个几何体可能是(
A.四棱柱
B.五棱柱
C.六棱锥
D.七棱柱
D
)A.四棱柱
B.五棱柱
C.六棱锥
D.七棱柱
答案:
D
5. 如图,从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体,则剩余部分的体积和表面积分别是(
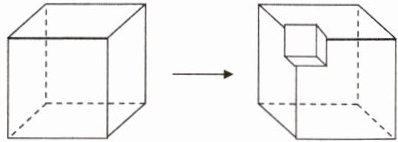
A.$27cm^{3},54cm^{2}$
B.$26cm^{3},54cm^{2}$
C.$27cm^{3},51cm^{2}$
D.$26cm^{3},51cm^{2}$
B
)
A.$27cm^{3},54cm^{2}$
B.$26cm^{3},54cm^{2}$
C.$27cm^{3},51cm^{2}$
D.$26cm^{3},51cm^{2}$
答案:
B
6. 用一个平面去截一个正方体,截面的边数最多是
6
.
答案:
6
7. 用一个平面去截一个几何体,所得的截面是四边形,则这个几何体可能是下列几何体中的
(1)圆柱;(2)圆锥;(3)三棱柱;(4)三棱锥;(5)五棱锥.
(1)(3)(4)(5)
.(填序号)(1)圆柱;(2)圆锥;(3)三棱柱;(4)三棱锥;(5)五棱锥.
答案:
(1)
(3)
(4)
(5)
(1)
(3)
(4)
(5)
8. 一个正方体用平面截去一个角后,则剩余几何体最多有
10
个顶点,15
条棱,7
个面.
答案:
10 15 7
9. 在手工课上,需要将一个四棱柱形的橡皮泥变成两块棱柱,要求只切一刀,这两个棱柱可能是几棱柱呢?
答案:
解:如图所示,这两个棱柱可能是两个四棱柱,或两个三棱柱,或一个五棱柱、一个三棱柱,或一个四棱柱、一个三棱柱.
解:如图所示,这两个棱柱可能是两个四棱柱,或两个三棱柱,或一个五棱柱、一个三棱柱,或一个四棱柱、一个三棱柱.

按下列方式截正方体,能得到什么样的几何图形,请在图(5)中画出截面是梯形的示意图.




答案:
解:如图: (画法不唯一).
(画法不唯一).
解:如图:
 (画法不唯一).
(画法不唯一). 查看更多完整答案,请扫码查看


