《2025年伴你学江苏七年级数学上册苏科版》

1. 小敏放学回家自己煮面条吃.有下面几道工序：① 洗锅盛水(2 min)；② 洗菜(3 min)；③ 准备面条及佐料(2 min)；④ 烧水(7 min)；⑤ 用烧开的水煮面条和菜(3 min).其中,除④外,一次只能进行一道工序.要将面条煮好,最少需要几分钟？用合适的方式表达煮面条的过程.

答案： 解:可在烧水时洗菜和准备面条,因此①④⑤是必须做的
2+7+3=12(min)
答：最少需要12分钟。

2. 观察下列等式,并回答问题.
第1个等式$\frac{2}{1}= \frac{1}{1}+\frac{1}{1}$；第2个等式$\frac{2}{3}= \frac{1}{2}+\frac{1}{6}$；第3个等式$\frac{2}{5}= \frac{1}{3}+\frac{1}{15}$；第4个等式$\frac{2}{7}= \frac{1}{4}+\frac{1}{28}$；第5个等式$\frac{2}{9}= \frac{1}{5}+\frac{1}{45}$；…
(1)上述等式有怎样的规律？用合适的方式表达这个规律.
解:第n个等式:$\frac {2}{2n-1}=\frac {1}{n}+\frac {1}{n(2n-1)}$
(2)写出第6个等式：$\frac{2}{11}=\frac{1}{6}+\frac{1}{66}$.
(3)写出第10个等式：$\frac{2}{19}=\frac{1}{10}+\frac{1}{190}$.

答案： $​\frac{2}{11}=\frac{1}{6}+\frac{1}{66}​$
$​\frac{2}{19}=\frac{1}{10}+\frac{1}{190}​$
解:​第n个等式$:\frac {2}{2n-1}=\frac {1}{n}+\frac {1}{n(2n-1)}​$

3. 观察下面的点阵图和对应的等式,探究其中的规律.

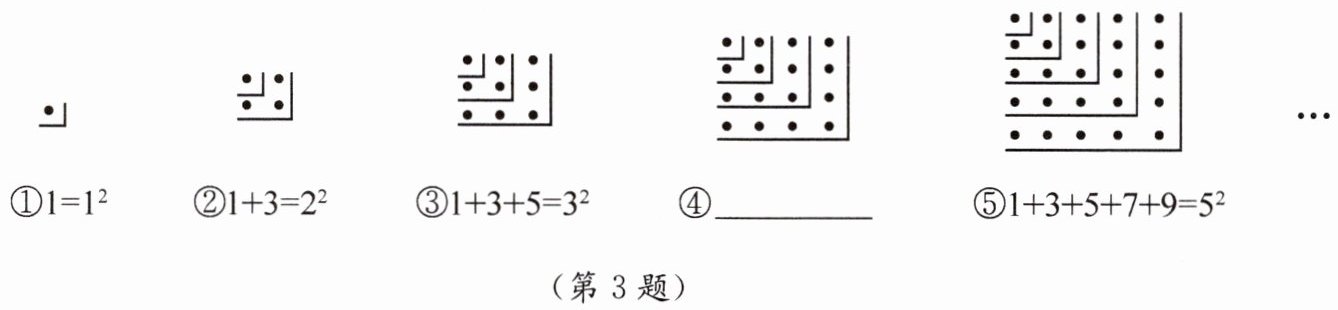
(1)写出与第④个图对应的等式：1+3+5+7=4²
(2)请写出与第n个图对应的等式；1+3+···+(2n-1)=n²
(3)利用(2)中的等式,计算：41+43+45+…+199.
解:原式=1+3+5+…+41+43+······199-(1+3+5+···+39)=100²-20²=9600

答案： $ $　　
$​ $解$:$　　
$(1)1+3+5+7=4^{2}​$　　
$​$　　
$(2)1+3+···+(2n-1)=n^{2}​$　　
$​$　　
$(3)$原式$=1+3+5+···+41+43+······199-(1+3+5+···+39)​$　　
$​=100^{2}-20^{2}​$　　
$​=9600​$