《2025年伴你学江苏七年级数学上册苏科版》

1. 把x= -2代入代数式$2x^{2}-x-1$后的算式为$2×(-2)^{2}-(-2)-1$.

答案： $2×(-2)^{2}-(-2)-1$　　

2. 若$2a^{2}+3b+6= 8$,求代数式$2a^{2}+3b-9$的值.

答案： 解$:$由题$,2a^{2}+3b=8-6=2$　　
则原式$=2-9=-7$　　

3. 已知$|a^{2}+b^{2}-3|= 5$,则$-3a^{2}-3b^{2}=$-24.

答案： -24

4. 在一种计算游戏中,规定$\begin{vmatrix} a&b\\ c&d\end{vmatrix} = ad-bc$,则$\begin{vmatrix} 1&2\\ 3&4\end{vmatrix} $的值是-2.

答案： -2

5. 若a,b互为相反数,c,d互为倒数,$|m|= 4$,求代数式$(a+b)-dc+2cd-m^{2}+\frac{b}{a}$的值.

答案： 解:由题,a+b=0,cd=1,m=±4
∴原式=0-1+2-16+(-1)=-16

1. 小张在计算31+a的值时,误将“+”号看成“-”号,结果得12,那么31+a的值应为50.

答案： 50

2. 某通信套餐的电话费与通话时间的关系如右表：

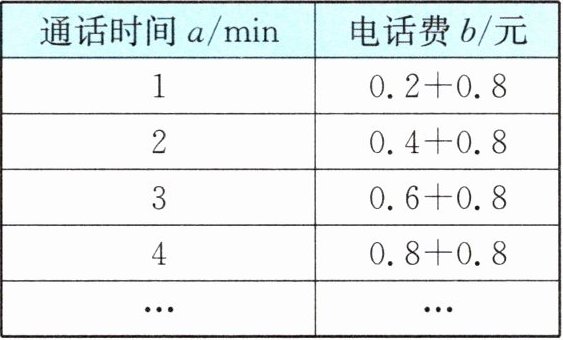
(1)试用含a的代数式表示b；
(2)当a= 100时,计算b的值.

答案： 解:
(1)b=0.2a+0.8
(2)b=0.2×100+0.8=20.8

3. 当x= 1时,代数式$px^{2}+qx+1$的值为2023. 请求出当x= -1时,代数式$px^{2}+qx+1$的值.

答案： 解:由题,p+q+1=2023,
∴p+q=2022
把x=-1代入原式=-p-q+1=-(p+q)+1=-2022+1=-2021

4. 根据表中弹簧长度与悬挂物体的质量的对应值,解答下列问题(假设均在弹簧弹性限度内)：

(1)用代数式表示所挂物体的质量为x kg时的弹簧长度l(cm).
(2)所挂物体的质量为10 kg时,弹簧长度是多少？
(3)若测得弹簧长度是18 cm,则所挂物体的质量为多少？
(4)观察表格,随着悬挂物体的质量x逐渐增大,弹簧长度l如何变化？

答案： 解:
(1)l=(0.5x+12)cm
(2)把x=10代入有,l=0.5×10+12=17,
∴为17cm
(3)把l=18代入有,18=0.5x+12,解得x=12,
∴为12kg
(4)l随着x的增大而增大