《2025年伴你学江苏七年级数学上册苏科版》

6. 计算：
(1)$-1^{2023}-\left[2× (-1)^{2}-3^{2}\right]÷ (-6)$；
(2)$\left(\frac{11}{12}-\frac{7}{6}+\frac{3}{4}-\frac{13}{24}\right)× (-48)$.

答案：
(1)
$\;\;\;-1^{2023}-\left[2× (-1)^{2}-3^{2}\right] ÷ (-6)$
$=-1 - \left[2× 1 - 9\right] ÷ (-6)$
$=-1 - \left[2 - 9\right] ÷ (-6)$
$=-1 - (-7) ÷ (-6)$
$=-1 - \frac{7}{6}$
$=-1 - 1\frac{1}{6}$
$=-2\frac{1}{6}$
$=-\frac{13}{6}$
(2)
$\;\;\;\left(\frac{11}{12}-\frac{7}{6}+\frac{3}{4}-\frac{13}{24}\right)× (-48)$
$=\frac{11}{12}× (-48) - \frac{7}{6}× (-48) + \frac{3}{4}× (-48) - \frac{13}{24}× (-48)$
$=-44 + 56 - 36 + 26$
$=2$

7. 如图,数轴上的点$A$,$B$,$O$,$C$,$D分别表示-5$,$-1.5$,$0$,$2.5$,$6$,据此回答下列问题：

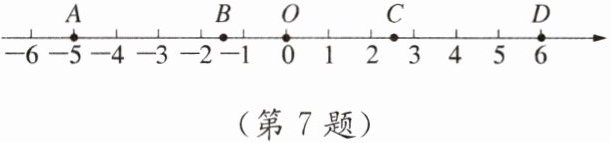
(1)$C$,$B$两点间的距离是多少？
(2)到点$A$的距离等于 6 的点表示的数是多少？
(3)到$A$,$D$两点的距离相等的点表示的数是多少？

答案：
(1) 因为点$B$表示$-1.5$，点$C$表示$2.5$，所以$C$，$B$两点间的距离是$|2.5 - (-1.5)| = |2.5 + 1.5| = 4$。
(2) 设到点$A$的距离等于$6$的点表示的数是$x$，点$A$表示$-5$，则$|x - (-5)| = 6$，即$|x + 5| = 6$。当$x + 5 = 6$时，$x = 1$；当$x + 5 = -6$时，$x = -11$。所以该点表示的数是$1$或$-11$。
(3) 设到$A$，$D$两点的距离相等的点表示的数是$y$，点$A$表示$-5$，点$D$表示$6$，则$|y - (-5)| = |y - 6|$，即$|y + 5| = |y - 6|$。当$y + 5 = y - 6$时，方程无解；当$y + 5 = -(y - 6)$时，$y + 5 = -y + 6$，$2y = 1$，$y = 0.5$。所以该点表示的数是$0.5$。
(1) $4$
(2) $1$或$-11$
(3) $0.5$

8. 快递员小张在东西方向的路上送快递,以快递站所在位置为原点,方向向东为正. 某天他骑车从快递站出发向东行驶了 2 km 到达李村,再向东行驶了 4 km 到达郭庄,然后又向西行驶了 10 km 到达王庄,最后回到快递站.
(1)画出表示小张送快递路线的数轴；
(2)小张骑行的路程是多少？

答案：
(1) （此处需画图，因无法直接绘制数轴，故实际作答时应画出以快递站为原点，向东为正方向的数轴，标注出李村（+2）、郭庄（+6）、王庄（-4）的位置及行驶路线）
(2) 2 + 4 + 10 + 4 = 20(km)
答：小张骑行的路程是20km。