《2025年伴你学江苏七年级数学上册苏科版》

1. 下列变形中不正确的是(D)
A.若$x= y$,则$x+5= y+5$
B.若$x= y$,则$10x= 10y$
C.若$a+1= b+1$,则$a= b$
D.若$x= y$,则$\frac{x}{a}= \frac{y}{a}$

答案： D

2.(1)已知等式$3x= 2x-1$,两边同时减2x,得$x=$-1,依据是等式基本性质1；
(2)已知等式$-\frac{1}{3}x= 2$,两边同时乘-3,得$x=$-6,依据是等式基本性质2.

答案： 减2x
-1
等式基本性质1
乘-3
-6
等式基本性质2

3. 利用等式的基本性质,将下面的等式变形为$x= c$($c$为常数)的形式.
(1)$x-9= 6$；
(2)$-0.2x= 10$；
(3)$3-\frac{1}{3}x= 2$；
(4)$-2x+1= 0$.

答案： 解$: x-9+9=6+9$　　
$ x=15$　　
解$: -0.2x÷(-0.2)=10÷(-0.2)$　　
$ x=-50$　　
$ $解$:\ 3-\frac {1}{3}x+\frac {1}{3}x-2=2+\frac {1}{3}x-2$　　
$\ \ \ \ \ \ \frac {1}{3}x×3=1×3\ $　　
$\ \ \ \ \ \ \ \ \ \ \ \ \ x=3$　　
解$:\ \ -2x+1-1=0-1$　　
$\ \ \ \ \ \ -2x÷(-2)=-1÷(-2)$　　
$\ \ \ \ \ \ \ x=\frac {1}{2}$　　

1. 根据下列情境中的等量关系列出一个等式.
(1)原价为$a$元的某商品降价10%后恰好比原价的一半多80元.
(2)已知铅笔每支$m$元,练习本每本$n$元,买4本练习本和5支铅笔一共用了4.9元.
(3)某商店销售一批服装,已知服装的成本价为每件$m$元,每件标价150元,打八折后出售,仍可获利$b$元.
(4)A,B两地相距480 km,一辆轿车以100 km/h的速度从A地出发匀速行驶,前往B地. 同时,一辆货车以80 km/h的速度从B地出发匀速行驶,前往A地. $x$ h后两车相遇.

答案： 解$:(1)(1-10\%)a=\frac{1}{2}a+80$
(2)4n+5m=4.9
(3)150×0.8-m=b
(4)100x+80x=480

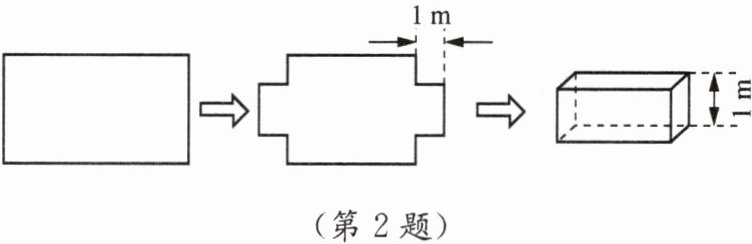
2. 如图,将一块长方形铁皮的四个角各剪去一个边长为1 m的正方形后,剩下的部分刚好能围成一个容积为$15\ m^3$的无盖长方体箱子,且此箱子底面的长比宽多2 m. 设该长方体箱子底面的宽为$x$ m.
(1)用含$x$的代数式分别表示该长方体箱子底面的长和箱子的容积；
(2)请根据等量关系列出一个等式.

答案：  
解:
(1)长为x+2
容积为x(x+2)
(2)x(x+2)=15