第19页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
4.(1)$-2$的绝对值是
(2)绝对值不大于3的非负整数是
2
,$\frac{2}{3}$的绝对值是$\frac{2}{3}$
,绝对值等于3的数是±3
;(2)绝对值不大于3的非负整数是
0,1,2,3
.
答案:
2
$\frac{2}{3}$
±3
0,1,2,3
$\frac{2}{3}$
±3
0,1,2,3
5. 已知$|a|= \left|-\frac{1}{2}\right|$,那么$a$的值是
$±\frac{1}{2}$
.
答案:
$±\frac{1}{2}$
6. 用“>”“<”或“=”填空:
(1)$-1$
(2)$-|-2|$
(3)$-0.3$
(4)$-\left(-\frac{1}{9}\right)$
(1)$-1$
<
$-0.01$;(2)$-|-2|$
<
0;(3)$-0.3$
>
$-\frac{1}{3}$;(4)$-\left(-\frac{1}{9}\right)$
>
$-\left|-\frac{1}{10}\right|$.
答案:
<
<
>
>
<
>
>
1. 若$|a-2|+|b-7|= 0$,则$b-a= $
5
.
答案:
5
2. 如图,四个有理数在数轴上的对应点分别为$M$,$P$,$N$,$Q$.若点$M$,$N$表示的有理数互为相反数,则点$M$,$P$,$N$,$Q$中,表示的数的绝对值最小的点是
P
.
答案:
P
3. 我们知道,对于有理数$a$,当$a>0$时,$|a|= a$;当$a<0$时,$|a|= -a$;当$a= 0$时,$|a|= a$.由此可知,对于$a-b$,若$a>b$,则$a-b>0$,即$|a-b|= a-b$;若$a<b$,则$a-b<0$,即$|a-b|= b-a$;若$a= b$,则$a-b= 0$,即$|a-b|= 0$.据此回答问题:
(1)在$|x-1|$中,当$x>1$时,$x-1$
(2)在$|x-1|$中,当$x<1$时,$x-1$
(3)在$|x-1|$中,当$x= 1$时,$x-1$
(4)数$a$,$b$,$c$在数轴上表示的点如图所示,则$|b-a|= $
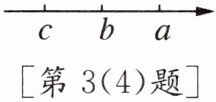
(1)在$|x-1|$中,当$x>1$时,$x-1$
>
0,$|x-1|= $x-1
;(2)在$|x-1|$中,当$x<1$时,$x-1$
<
0,$|x-1|= $1-x
;(3)在$|x-1|$中,当$x= 1$时,$x-1$
=
0,$|x-1|= $0
;(4)数$a$,$b$,$c$在数轴上表示的点如图所示,则$|b-a|= $
a-b
,$|b-c|= $b-c
.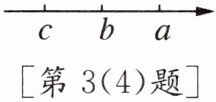
答案:
>
x-1
<
1-x
=
0
a-b
b-c
>
x-1
<
1-x
=
0
a-b
b-c
4. 请阅读材料,并解决问题.
在比较$-\frac{99}{201}与-\frac{51}{101}$的大小时,若利用绝对值法比较,则需要进行分数的通分,因为分母较大,所以比较烦琐.我们也可以使用如下的方法比较大小:
因为$\frac{99}{201}<\frac{1}{2}$,$\frac{51}{101}>\frac{1}{2}$,所以$\frac{99}{201}<\frac{51}{101}$,所以$-\frac{99}{201}>-\frac{51}{101}$.
(1)填空:上述方法是先通过找中间量
(2)利用上述方法比较$-\frac{43}{126}与-\frac{79}{243}$的大小.
解:因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
在比较$-\frac{99}{201}与-\frac{51}{101}$的大小时,若利用绝对值法比较,则需要进行分数的通分,因为分母较大,所以比较烦琐.我们也可以使用如下的方法比较大小:
因为$\frac{99}{201}<\frac{1}{2}$,$\frac{51}{101}>\frac{1}{2}$,所以$\frac{99}{201}<\frac{51}{101}$,所以$-\frac{99}{201}>-\frac{51}{101}$.
(1)填空:上述方法是先通过找中间量
$\frac{1}{2}$
来比较正数$\frac{99}{201}与\frac{51}{101}$的大小,再根据两个负数比较大小的结论“绝对值
大的负数反而小”进行判断.(2)利用上述方法比较$-\frac{43}{126}与-\frac{79}{243}$的大小.
解:因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
答案:
$\frac{1}{2}$
绝对值
解$:-\frac{43}{126}<-\frac{79}{243}$
因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
绝对值
解$:-\frac{43}{126}<-\frac{79}{243}$
因为$\frac{43}{126}>\frac{1}{3},\frac{79}{243}<\frac{1}{3}$
所以$\frac{43}{126}>\frac{79}{243}$
所以$-\frac{43}{126}<-\frac{79}{243}$
查看更多完整答案,请扫码查看


