《2025年伴你学江苏七年级数学上册苏科版》

活动二：搭一搭
如图1-2,每个图形都是由小正方形和实心圆按一定规律排列而成的.按此规律继续排列.
(1)第20个图形中有42个实心圆.
(2)请完成下表:
68101214···32
(3)每增加一个小正方形,实心圆的数量怎么变化?
解:
(3)每增加一个小正方形，实心圆个数增加2
(4)你能发现每个图形中实心圆个数和小正方形个数之间的关系吗?
(4)实心圆个数比小正方形个数的2倍多2个

答案： 42
6
8
10
12
14
···
32
解:
(3)每增加一个小正方形，实心圆个数增加2
(4)实心圆个数比小正方形个数的2倍多2个

活动三:看一看
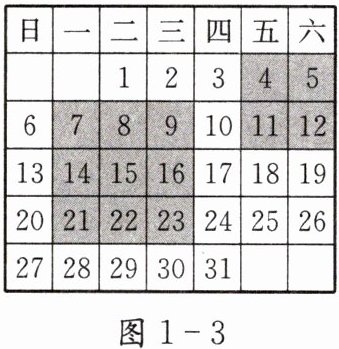
观察图1-3中的月历:
(1)月历中2×2涂色方框内的四个数有什么关系?
(2)月历中3×3涂色方框内的九个数有什么特征?是否存在3×3方框内的九个数满足和为108?请说明理由.
(3)小明一家外出旅游五天,这五天的日期之和是20,小明几号回到家?

答案：  
 
 
解:
(1)对角线的和相等
(2)和是中间数的9倍，若和为108，则中间的那个数必须是12，而12在该日历中不可能是中间数，
故9个数的和不可能是108
(3)20÷5=4，则中间第3天是4日,6 日回到家