《2025年伴你学江苏七年级数学上册苏科版》

2. 用代数式表示“a与b的平方的和”为 (B)
A.$(a+b)^2$
B.$a+b^2$
C.$a^2+b$
D.$a^2+b^2$

答案： B

3. 用代数式表示下列数量,不恰当的有①②③(填序号).
① 长为a、宽为$1\frac{1}{2}的长方形面积记为1\frac{1}{2}a$；
② 长、宽、高分别为2,x,y的长方体体积记为$2×x×y$；
③ 苹果a元/kg,买3b kg苹果需要a3b元；
④ 儿子的年龄是x岁,父亲的年龄是儿子的2倍多3岁,父亲年龄为(2x+3)岁.

答案： ①②③
①代数式中有字母时不能使用带分数,会造成歧义
②字母相乘的最终结果省略乘号
③数字写在字母前面

4. 在甲商店累计购物超过200元后,超出200元的部分按八五折收费；在乙商店累计购物超过100元后,超出100元的部分按九折收费.现某顾客累计购物x元(x＞200),若在甲商店购物,则实际支付0.85x+30元；若在乙商店购物,则实际支付0.9x+10元.(均用含x的代数式表示)

答案： (0.85x+30)
(0.9x+10)

1. 填空题：
(1)“x的5倍与y的和的一半”可以表示为$\frac{1}{2}(5x+y)$；
(2)“与m-3的积是5的数”可以表示为$\frac{5}{m-3}$；
(3)甲、乙两车分别以v km/h和u km/h的速度同时从A,B两地相向而行,3 h后两车相遇,则A,B两地相距(3v+3u)km；
(4)电影院第一排有m个座位,若每一排都比前一排多1个座位,则第n排的座位数是m+n-1.

答案： $​\frac{1}{2}(5x+y)​$
$​\frac{5}{m-3}​$
(3v+3u)
m+n-1

2. (1)用含a,b的代数式表示相应图形的面积.

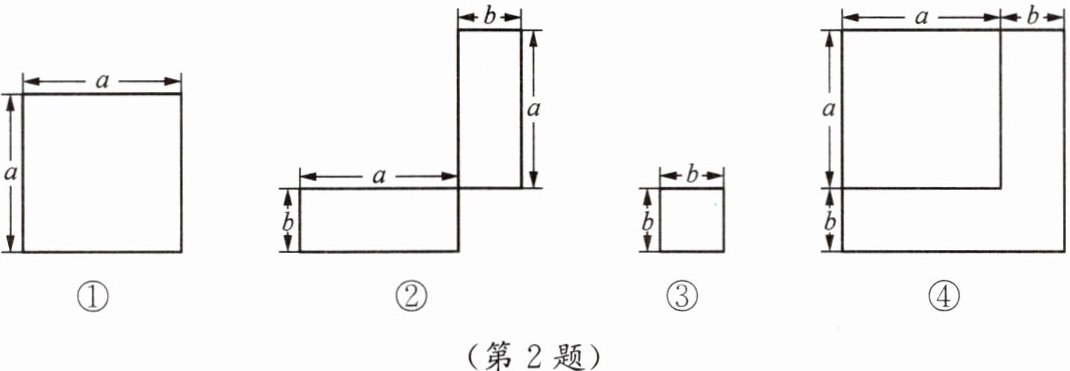
①$a^{2}$； ②$2ab$； ③$b^{2}$； ④$(a+b)^2$.
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表示：$a^{2}+2ab+b^{2}=(a+b)^{2}$.

答案： $ $　　
$​ a^{2}​$　　
$2ab$　　
$​ b^{2}​$　　
$​a^{2}+2ab+b^{2}=(a+b)^{2}​$