《2025年伴你学江苏七年级数学上册苏科版》

1. 填空：
(1)$(-2)^{6}$读作(-2)的6次方,表示6个(-2)相乘,其中指数为6,底数为-2；
(2)$-2^{6}$读作2的6次方的相反数,表示6个2相乘的积的相反数,其中指数为6,底数为2.

答案： (-2)的6次方
6个(-2)相乘
6
-2
2的6次方的相反数
6个2相乘的
积的相反数
6
2

2. $\frac{49}{121}= $$±\frac{7}{11}$$^{2}$,$(-2×4)^{3}= $-512.

答案： $±\frac{7}{11}$
-512

3. 下列各组数中,运算结果相同的是(C)
A.$3^{4}和4^{3}$
B.$-3^{2}和(-3)^{2}$
C.$(-2)^{3}和-2^{3}$
D.$(-\frac{2}{3})^{2}和(-\frac{3}{2})^{2}$

答案： C

4. 下列说法中,正确的有(B)
① 对于任意有理数m,都有$m^{2}＞0$；② 对于任意有理数m,都有$m^{2}= (-m)^{2}$；③ 对于任意有理数m,n(m≠n),都有$(m-n)^{2}＞0$；④ 对于任意有理数m,都有$m^{3}= (-m)^{3}$.
A.1个
B.2个
C.3个
D.0个

答案： B

5. 计算：(1)$(-5)^{2}$； (2)$(-0.1)^{4}$； (3)$(-\frac{2}{3})^{3}$； (4)$(-\frac{1}{5})^{3}$.

答案：
(1)
$(-5)^{2} = (-5) × (-5) = 25$
(2)
$(-0.1)^{4} = (-0.1) × (-0.1) × (-0.1) × (-0.1) = 0.0001$
(3)
$\left(-\frac{2}{3}\right)^{3} = \left(-\frac{2}{3}\right) × \left(-\frac{2}{3}\right) × \left(-\frac{2}{3}\right) = -\frac{8}{27}$
(4)
$\left(-\frac{1}{5}\right)^{3} = \left(-\frac{1}{5}\right) × \left(-\frac{1}{5}\right) × \left(-\frac{1}{5}\right) = -\frac{1}{125}$

1. 下列算式中,结果为正数的是(B)
A.$-(-4)^{2}$
B.$-(-4^{2})$
C.$-|-4|^{2}$
D.$-[-(-4)]$

答案： B

2. 观察下列数据,按规律在横线上填写适当的数：
1,$-\frac{3}{4}$,$\frac{5}{9}$,$-\frac{7}{16}$,$\frac{9}{25}$,$-\frac{11}{36}$,…

答案： $-\frac{11}{36}$

3. 用“＜”将$\frac{1}{4}$,0,$-\frac{2}{3}$,$(-\frac{1}{5})^{2}$,$(-3)^{3}$按从小到大的顺序排列：$(-3)^{3},-\frac{2}{3},0,(-\frac{1}{5})^{2},\frac{1}{4}$.

答案： $(-3)^{3},-\frac{2}{3},0,(-\frac{1}{5})^{2},\frac{1}{4}$

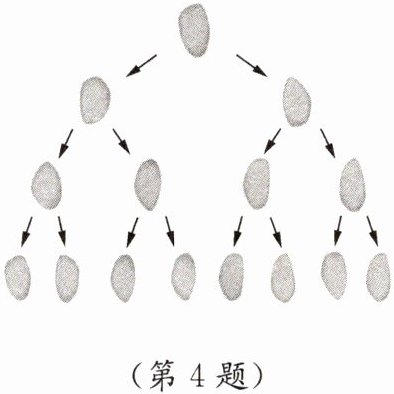
4. 细菌通过分裂的方式进行繁殖,1个细菌分裂成2个细菌,这2个细菌又分别能分裂成2个细菌……如图是某种细菌分裂的示意图,已知该种细菌每20 min能分裂一次,则1个该种细菌经过3 h可以分裂成512个细菌.

答案： 512