《2025年同步练习上海科学技术出版社七年级数学上册沪科版》

8. 某中学七年级(1)班 $ 4 $ 名教师决定带领本班 $ m $ 名学生去某地参观。该地每张门票的票价为 $ 30 $ 元,现有 $ A $、$ B $ 两种购票方案可供选择：
方案 $ A $：教师全价,学生半价；
方案 $ B $：不分教师与学生,全部六折优惠。
(1) 请用含 $ m $ 的代数式分别表示选择 $ A $,$ B $ 两种方案所需的费用；
(2) 当学生人数 $ m = 40 $ 时,且只选择其中一种方案购票,请通过计算说明选择哪种方案更为优惠。

答案： 1. （1）
方案$A$：
教师有$4$名，教师全价，每张门票$30$元，学生有$m$名，学生半价，即每张门票$30×0.5 = 15$元。
那么方案$A$所需费用$y_{A}=30×4 + 15m$，化简得$y_{A}=120 + 15m$。
方案$B$：
总人数为$(m + 4)$人，全部六折优惠，每张门票$30×0.6=18$元。
那么方案$B$所需费用$y_{B}=30×0.6×(m + 4)$，展开式子：
$y_{B}=18×(m + 4)=18m+72$。
2. （2）
当$m = 40$时：
方案$A$：
把$m = 40$代入$y_{A}=120 + 15m$，得$y_{A}=120+15×40$。
先算乘法：$15×40 = 600$，再算加法：$y_{A}=120 + 600=720$（元）。
方案$B$：
把$m = 40$代入$y_{B}=18m + 72$，得$y_{B}=18×40+72$。
先算乘法：$18×40 = 720$，再算加法：$y_{B}=720+72 = 792$（元）。
因为$720\lt792$，所以当$m = 40$时，选择方案$A$更为优惠。
综上，（1）方案$A$费用$y_{A}=15m + 120$，方案$B$费用$y_{B}=18m + 72$；（2）选择方案$A$更为优惠。

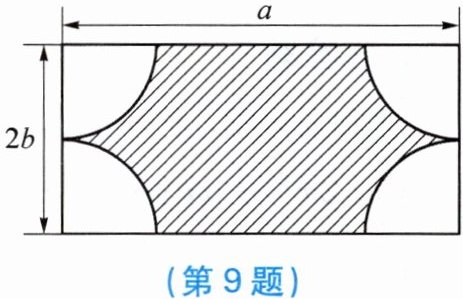
9. 下图是某居民小区的一块长为 $ a m $、宽为 $ 2b m $ 的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为 $ b m $ 的扇形花台,然后在花台内种花,其余种草。如果建造花台及种花的费用为 $ 100 $ 元/$ m^{2} $,种草的费用为 $ 50 $ 元/$ m^{2} $。
(1) 美化这块空地共需多少元(用含有 $ a $,$ b $,$ π $ 的式子表示)？
(2) 当 $ a = 6 $,$ b = 2 $,$ π $ 取 $ 3 $ 时,美化这块空地共需多少元？

答案： 1. （1）
首先求花台的面积和种草部分的面积：
因为四个顶点处的扇形花台半径为$b m$，且四个扇形的圆心角之和为$360^{\circ}$，所以花台的面积$S_{花台}=\pi b^{2}$（根据圆的面积公式$S = \pi r^{2}$，这里$r = b$）。
长方形空地的面积$S_{长方形}=a×2b = 2ab$。
则种草部分的面积$S_{种草}=S_{长方形}-S_{花台}=2ab-\pi b^{2}$。
然后求总费用：
建造花台及种花的费用为$100$元$/m^{2}$，种草的费用为$50$元$/m^{2}$。
总费用$W = 100×\pi b^{2}+50×(2ab - \pi b^{2})$。
展开式子：
$W = 100\pi b^{2}+100ab-50\pi b^{2}$。
合并同类项得$W=(50\pi b^{2}+100ab)$元。
2. （2）
当$a = 6$，$b = 2$，$\pi = 3$时：
把值代入$W = 50\pi b^{2}+100ab$中。
$W=50×3×2^{2}+100×6×2$。
先计算$50×3×2^{2}$：
$50×3×2^{2}=50×3×4 = 600$。
再计算$100×6×2=1200$。
则$W=600 + 1200=1800$元。
综上，（1）美化这块空地共需$(50\pi b^{2}+100ab)$元；（2）当$a = 6$，$b = 2$，$\pi$取$3$时，美化这块空地共需$1800$元。