《2025年同步练习上海科学技术出版社七年级数学上册沪科版》

1. 计算$(-2)^{2023} + (-2)^{2024}$所得的结果为(A).
A.$2^{2023}$
B.$(-2)^{2023}$
C.$-2^{2023}$
D.$-2$

答案： A

2. 当$a ＜ 0$时,下列等式成立的有(C).
① $a^{2} = (-a)^{2}$; ② $a^{3} = -(-a)^{3}$; ③ $a^{2} = |a^{2}|$; ④ $a^{3} = |a^{3}|$.
A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： C

3. 在生态系统中,每输入一个营养级的能量,大约有$10\%$的能量流到下一个营养级. 在$H_{1} \to H_{2} \to H_{3} \to H_{4} \to H_{5} \to H_{6}$这条生物链中($H_{n}表示第n$个营养级,$n = 1,2,3,\ldots,6$),要使$H_{6}获得10 kJ$的能量,那么需要$H_{1}$提供的能量约是(C).
A.$10^{4} kJ$
B.$10^{5} kJ$
C.$10^{6} kJ$
D.$10^{7} kJ$

答案： C

4. 当$a = -1$时,$a + a^{2} + a^{3} + … + a^{100} = $0.

答案： 0

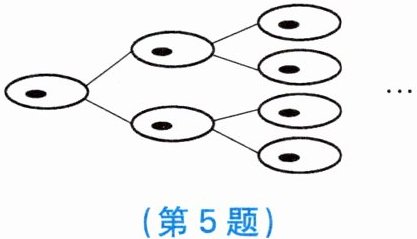
5. 右图是某种细胞分裂示意图,这种细胞每过$30 min便由1个分裂成2$个. 根据此规律可得：
(1) 这样的一个细胞经过第$4个30 min$后可分裂成16个细胞；
(2) 这样的一个细胞经过$3 h$后可分裂成64个细胞；
(3) 这样的一个细胞经过$n h$后可分裂成$2^{2n}$个细胞($n$为正整数).

答案：
(1)16；
(2)64；
(3)$2^{2n}$

6. 我们常用的数是十进制数,如$2639 = 2 × 10^{3} + 6 × 10^{2} + 3 × 10^{1} + 9$. 表示十进制的数要用$10$个数码：$0$, $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$, $9$. 在电子计算机中用的是二进制,只要用两个数码：$0和1$,如二进制中的$101等于十进制的5$,即$101_{(2)} = 1 × 2^{2} + 0 × 2^{1} + 1$,二进制中的$10111等于十进制的23$,即$10111_{(2)} = 1 × 2^{4} + 0 × 2^{3} + 1 × 2^{2} + 1 × 2^{1} + 1$,那么二进制中的$1101$等于十进制中的数是13.

答案： 13

7. 计算：
(1) $|-8| + 2^{2} + (-3)^{2} - (-1)^{3}$;
(2) $\left(\frac{1}{2}\right)^{3} × 9 × 8 - 3 ÷ (-1)^{3}$.

答案： 1. （1）
解：
先分别计算各项：
根据绝对值的性质$\vert - 8\vert=8$；
根据乘方的定义$2^{2}=4$，$(-3)^{2}=(-3)×(-3)=9$，$(-1)^{3}=(-1)×(-1)×(-1)= - 1$。
然后代入原式计算：
$\vert - 8\vert+2^{2}+(-3)^{2}-(-1)^{3}=8 + 4+9-(-1)$。
根据有理数的减法法则$a-(-b)=a + b$，则$8 + 4+9-(-1)=8 + 4+9 + 1$。
按照从左到右的顺序计算：$8+4=12$，$12 + 9=21$，$21+1=22$。
2. （2）
解：
先分别计算各项：
根据乘方的定义$(\frac{1}{2})^{3}=\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{1}{8}$，$(-1)^{3}=-1$。
然后代入原式计算：
$(\frac{1}{2})^{3}×9×8-3÷(-1)^{3}=\frac{1}{8}×9×8-3÷(-1)$。
根据乘法交换律$a× b× c=a× c× b$，$\frac{1}{8}×9×8=\frac{1}{8}×8×9$，$\frac{1}{8}×8 = 1$，$1×9 = 9$；
根据有理数的除法法则$a÷(-b)=-a÷ b$，$3÷(-1)=-3$。
则$\frac{1}{8}×9×8-3÷(-1)=9-(-3)$。
根据有理数的减法法则$a-(-b)=a + b$，$9-(-3)=9 + 3=12$。
综上，（1）的结果是$22$；（2）的结果是$12$。