第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 数$a$,$b$,$c$在数轴上的位置如图所示,下列结论错误的是(
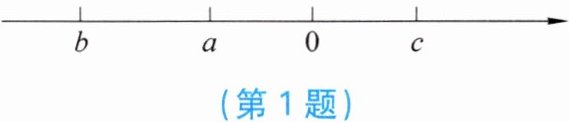
A.$ac + b<0$
B.$a + b + c<0$
C.$abc<0$
D.$ab + c>0$
C
).
A.$ac + b<0$
B.$a + b + c<0$
C.$abc<0$
D.$ab + c>0$
答案:
C
2. 已知$\vert x\vert = 3$,$\vert y\vert = 2$,且$x\cdot y<0$,则$x + y$的值等于(
A.$5或-5$
B.$1或-1$
C.$5或-1$
D.$-5或-1$
B
).A.$5或-5$
B.$1或-1$
C.$5或-1$
D.$-5或-1$
答案:
B
3. 超市推出如下优惠方案:① 一次性购物不超过$100$元,不享受优惠;② 一次性购物超过$100$元,但不超过$300$元,一律九折;③ 一次性购物超过$300$元,一律八折.某人两次购物分别付款$80元和252$元,如果他将这两次所购商品一次性购买,则应付款(
A.$288$元
B.$332$元
C.$288元或316$元
D.$332元或363$元
C
).A.$288$元
B.$332$元
C.$288元或316$元
D.$332元或363$元
答案:
C
4. 有一种“二十四点”的游戏,其游戏规则是:任取四个$1\sim13$之间的自然数,将这四个数(每个数用且只用一次)进行加减乘除四则运算,使其结果等于$24$.例如$1$,$2$,$3$,$4$,可作如下运算:$(1 + 2 + 3)×4 = 24$[注意上述运算与$4×(2 + 3 + 1)$应视作相同方法的运算].将上述规则扩展到四个有理数$3$,$4$,$-6$,$10$,写出三种不同方法的运算式,使其结果等于$24$.运算式如下:(1)
$10 - 4 - 3×(-6)$
;(2)$4 - 10×(-6)÷3$
;(3)$3×[10 + 4 + (-6)]$
.另有四个数$3$,$-5$,$7$,$-13$,可通过运算式:(4)$[(-5)×(-13) + 7]÷3$
使其结果等于$24$.
答案:
(1)$10 - 4 - 3×(-6)$ (2)$4 - 10×(-6)÷3$ (3)$3×[10 + 4 + (-6)]$ (4)$[(-5)×(-13) + 7]÷3$
5. 规定一种运算:$a\Delta b = 3ab$,如$2\Delta4 = 3×2×4 = 24$,则$(-4)\Delta5= $
-60
.
答案:
-60
6. 已知有理数$a$,$b$,$c$在数轴上的位置如图所示:
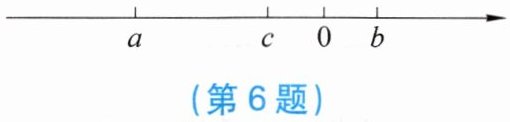
化简:$\frac{\vert abc\vert}{abc}+\frac{a + b + c}{\vert a + b + c\vert}-\frac{\vert bc\vert}{bc}-\frac{c - b}{\vert c - b\vert}-\frac{a}{\vert a\vert}=$

化简:$\frac{\vert abc\vert}{abc}+\frac{a + b + c}{\vert a + b + c\vert}-\frac{\vert bc\vert}{bc}-\frac{c - b}{\vert c - b\vert}-\frac{a}{\vert a\vert}=$
3
.
答案:
3
查看更多完整答案,请扫码查看


