《2025年辽宁作业分层培优学案八年级数学上册人教版》

13. 先化简,再求值：$(x + 2y)^2 - (x - 2y)^2 - (x + 2y)(x - 2y) - 4y^2$,其中 $x = -2$,$y = \dfrac{1}{2}$。

答案： 解:原式$=x^{2}+4xy+4y^{2}-(x^{2}-4xy+4y^{2})-(x^{2}-4y^{2})-4y^{2}$
$=x^{2}+4xy+4y^{2}-x^{2}+4xy-4y^{2}-x^{2}+4y^{2}-4y^{2}$
$=-x^{2}+8xy$.
当$x=-2,y=\frac{1}{2}$时,
原式$=-(-2)^{2}+8×(-2)×\frac{1}{2}=-4-8=-12$.

14. 阅读：已知 $a + b = 5$,$ab = 3$,求 $a^2 + b^2$ 的值。
解：$\because a + b = 5$,
$\therefore (a + b)^2 = 5^2$,即 $a^2 + 2ab + b^2 = 25$。
$\because ab = 3$,
$\therefore a^2 + b^2 = (a + b)^2 - 2ab = 19$。
参考上述过程解答：
(1) 若 $x - y = -3$,$xy = -2$。
①求 $x^2 + y^2$ 的值；
②求$(x + y)^2$的值。
(2) 已知 $x + y = 7$,$x^2 + y^2 = 25$,求$(x - y)^2$的值。

答案： 解:
(1)①$\because x-y=-3$,
$\therefore (x-y)^{2}=x^{2}-2xy+y^{2}=9$.
$\because xy=-2,\therefore x^{2}+y^{2}=5$.
②$\because x^{2}+y^{2}=5,xy=-2$,
$\therefore (x+y)^{2}=x^{2}+2xy+y^{2}=1$.
(2)$\because x+y=7$,
$\therefore (x+y)^{2}=x^{2}+2xy+y^{2}=49$.
$\because x^{2}+y^{2}=25,\therefore xy=12$,
$\therefore (x-y)^{2}=x^{2}-2xy+y^{2}=1$.

15. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则：两腰上的数都是 $1$,其余每个数均为其上方左右两数之和,它给出了$(a + b)^n$($n$ 为正整数)的展开式(按 $a$ 的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数 $1$,$2$,$1$,恰好对应$(a + b)^2 = a^2 + 2ab + b^2$展开式中的系数；第四行的四个数 $1$,$3$,$3$,$1$,恰好对应$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$展开式中的系数,等等。

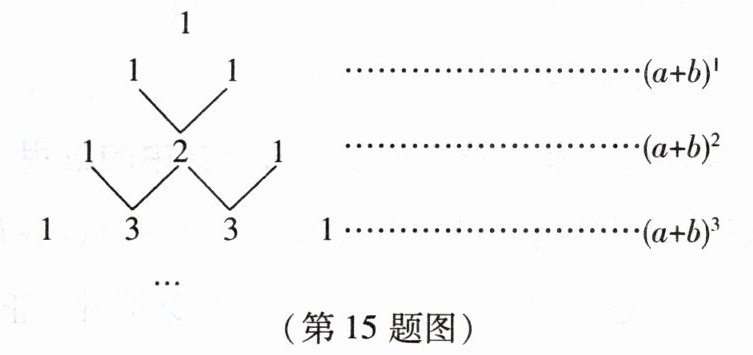
(1) 根据上面的规律,写出$(a + b)^5$的展开式；
(2) 利用上面的规律计算：$2^5 - 5×2^4 + 10×2^3 - 10×2^2 + 5×2 - 1$。

答案：
解:
(1)如图
　　　　　　
则$(a+b)^{5}=a^{5}+5a^{4}b+10a^{3}b^{2}+10a^{2}b^{3}+5ab^{4}+b^{5}$.
(2)$2^{5}-5×2^{4}+10×2^{3}-10×2^{2}+5×2-1$
$=2^{5}+5×2^{4}×(-1)+10×2^{3}×(-1)^{2}+10×2^{2}×(-1)^{3}+5×2×(-1)^{4}+(-1)^{5}$
$=(2-1)^{5}$
$=1$.