第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
1. 在$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle B = 80^{\circ}$,则$\angle C$的度数为(
A.$80^{\circ}$
B.$40^{\circ}$
C.$60^{\circ}$
D.$50^{\circ}$
B
)A.$80^{\circ}$
B.$40^{\circ}$
C.$60^{\circ}$
D.$50^{\circ}$
答案:
B
2. 一个三角形三个内角的度数之比为$1:3:5$,则最小的内角的度数为(
A.$20^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$60^{\circ}$
A
)A.$20^{\circ}$
B.$30^{\circ}$
C.$40^{\circ}$
D.$60^{\circ}$
答案:
A
3. 如图,$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle B = 40^{\circ}$,$DE // BC$,则$\angle AED$的度数是(
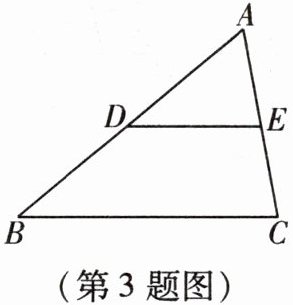
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
D
)
A.$50^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$80^{\circ}$
答案:
D
4. 如图,$\angle A = \frac{1}{2}\angle ABC = \frac{1}{2}\angle C$,$BD平分\angle ABC$,则$\angle DBC$的度数为
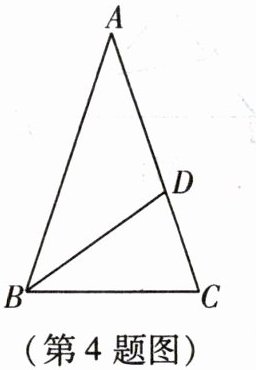
36°
。
答案:
36°
5.(新考法·创设真实情境)近年来,我国一直提倡“绿色环保、低碳生活”,健康骑行越来越受到人们的喜欢。自行车的示意图如图,其中$AB // CD$。若$\angle EAB = 60^{\circ}$,$\angle ECD = 40^{\circ}$,求$\angle AEC$的度数。
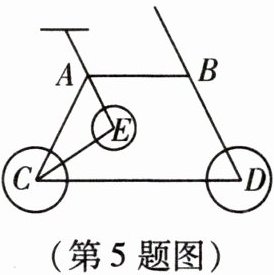

答案:
解:
∵AB//CD,
∴∠BAC+∠ACD=180°.
∵∠EAB=60°,∠ECD=40°,
∴∠EAC+∠ECA=180°-∠EAB-∠ECD=80°,
∴∠AEC=180°-(∠EAC+∠ACE)=100°.
∵AB//CD,
∴∠BAC+∠ACD=180°.
∵∠EAB=60°,∠ECD=40°,
∴∠EAC+∠ECA=180°-∠EAB-∠ECD=80°,
∴∠AEC=180°-(∠EAC+∠ACE)=100°.
6. 在$\triangle ABC$中,$\angle A = 20^{\circ}$,$\angle B = 4\angle C$,则$\angle C$等于(
A.$32^{\circ}$
B.$36^{\circ}$
C.$40^{\circ}$
D.$128^{\circ}$
A
)A.$32^{\circ}$
B.$36^{\circ}$
C.$40^{\circ}$
D.$128^{\circ}$
答案:
A
7. 如图,$\triangle ABC$中,$BF平分\angle ABC$,$CF平分\angle ACB$,$\angle BFC = 130^{\circ}$,则$\angle A$的度数为(

A.$80^{\circ}$
B.$70^{\circ}$
C.$60^{\circ}$
D.$45^{\circ}$
A
)
A.$80^{\circ}$
B.$70^{\circ}$
C.$60^{\circ}$
D.$45^{\circ}$
答案:
A
8. 如图,在$\triangle ABC$中,$\angle C = 70^{\circ}$,沿图中虚线截去$\angle C$,则$\angle 1 + \angle 2$等于(
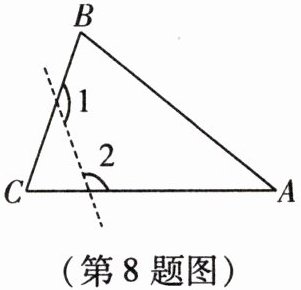
A.$360^{\circ}$
B.$250^{\circ}$
C.$180^{\circ}$
D.$140^{\circ}$
B
)
A.$360^{\circ}$
B.$250^{\circ}$
C.$180^{\circ}$
D.$140^{\circ}$
答案:
B
9. 如图是$A$,$B$,$C$三个村庄的平面图,已知$B村在A村的南偏西65^{\circ}15'$方向,$C村在A村的南偏东15^{\circ}$方向,$C村在B村的北偏东85^{\circ}$方向,则从$C村观测A$,$B两村的视角\angle ACB$的度数为

80°
。
答案:
80°
10.(新考法·跨物理学科)如图,两面镜子$AB$,$BC的夹角为\angle \alpha$,当光线经过镜子后反射,$\angle 1 = \angle 2$,$\angle 3 = \angle 4$。若$\angle \alpha = 68^{\circ}$,则$\angle \beta$的度数是
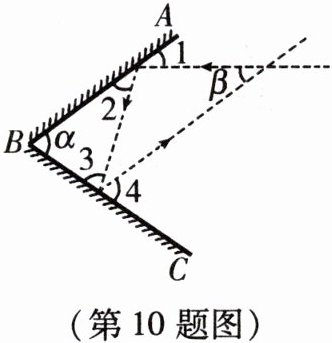
44°
。
答案:
44°
查看更多完整答案,请扫码查看


