《2025年辽宁作业分层培优学案八年级数学上册人教版》

11. 如图,在△ABC 中,AC 边上的高是(B)

A.线段 AD
B.线段 BE
C.线段 BF
D.线段 CF

答案： B

12. 下列说法错误的是(B)

A.锐角三角形的三条高交于一点
B.直角三角形只有一条高
C.钝角三角形有两条高在三角形的外部
D.任意三角形都有三条高、中线、角平分线

答案： B

13. 如图,△ABC 是边长为 1 个单位长度的正方形网格中的格点三角形,则其重心在(C)

A.线段 DE 上
B.线段 EF 上
C.线段 BE 上
D.线段 FG 上

答案： C

14. 如图,在△ABC 中,AD 是 BC 边上的中线,BE 是△ABD 中 AD 边上的中线,若△ABC 的面积是 24,则△ABE 的面积是6.

答案： 6

15. 如图,AD 是△ABC 的角平分线,P 为 AD 上一点,PM//AC 交 AB 于点 M,PN//AB 交 AC 于点 N. 求证：PA 平分∠MPN.

答案： 证明: $\because$ AD 是 $\triangle ABC$ 的角平分线,
$\therefore \angle BAD=\angle CAD$.
$\because PM// AC,PN// AB$,
$\therefore \angle APM=\angle CAD,\angle APN=\angle BAD$,
$\therefore \angle APM=\angle APN,\therefore PA$ 平分 $\angle MPN$.

16. 【探究学习】
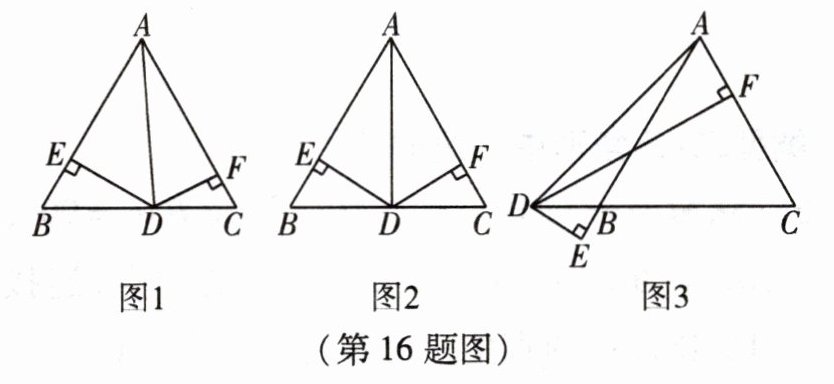
“用不同方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为“面积法”,请你利用“面积法”自主探究三角形高之间的数量关系.
【问题情境】
如图,在△ABC 中,AB = AC,D 为 BC 边所在直线上任意一点,连接 AD. 已知 DE,DF 分别是△ABD,△ACD 的高.
【解决问题】
(1)如图 1,当点 D 在边 BC 上时,请画出△ABC 中 AC 边上的高 BG.
(2)如图 1,通过观察、测量,猜想 DE,DF,BG 之间的数量关系为______；为了说明 DE,DF,BG 之间的数量关系,小明是这样做的：
证明：∵ $ S_{△ABC} $ = ______ + $ S_{△ACD} $,
∴ $ \frac{1}{2}AC \cdot BG = \frac{1}{2}AB \cdot DE + $______.
∵ AB = AC,∴______.
(3)如图 2,当 D 为 BC 的中点时,试判断 BG 与 DE 的数量关系,并说明理由.
(4)如图 3,当点 D 在 CB 的延长线上时,请直接写出 DE,DF,BG 之间的数量关系.
]

答案：
解:
(1) 如图1,BG 即为 AC 边上的高

(2) $BG=DE+DF$ $S_{\triangle ABD}$ $\frac{1}{2}AC\cdot DF$ $BG=DE+DF$
(3) $BG=2DE$.
理由: 如图2,过点 B 作 $BG\perp AC$ 于点 G.

$\because$ D 为 BC 的中点,
$\therefore S_{\triangle ABD}=S_{\triangle ACD}$.
$\because S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$,
$\therefore S_{\triangle ABC}=2S_{\triangle ABD}$,
$\therefore \frac{1}{2}AC\cdot BG=2×\frac{1}{2}AB\cdot DE$.
$\because AB=AC,\therefore BG=2DE$.
(4) 如图3,过点 B 作 $BG\perp AC$ 于点 G.

$\because S_{\triangle ADC}=S_{\triangle ADB}+S_{\triangle ACB}$,
$\therefore \frac{1}{2}AC\cdot DF=\frac{1}{2}AB\cdot DE+\frac{1}{2}AC\cdot BG$.
$\because AB=AC$,
$\therefore DF=DE+BG$.