《2025年辽宁作业分层培优学案八年级数学上册人教版》

8. 如图,直线AB//CD,且这两条直线的距离为8,∠AEF与∠EFC的平分线交于点P,则点P到EF的距离为4。

答案： 4

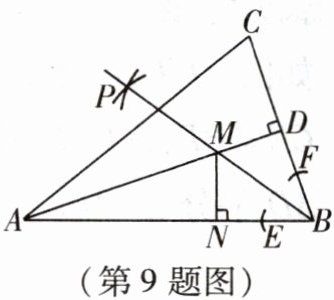
9. (湖南中考)如图,在锐角三角形ABC中,AD是边BC上的高,在BA,BC上分别截取线段BE,BF,使BE = BF；分别以点E,F为圆心,大于$\frac{1}{2}EF$的长为半径画弧,在∠ABC内,两弧交于点P,作射线BP,交AD于点M,过点M作MN⊥AB于点N。若MN = 2,AD = 4MD,则AM = 6。

答案： 6

10. 如图,在△ABC中,∠C = 90°。
(1)过点B作∠ABC的平分线交AC于点D；(尺规作图,保留作图痕迹)
(2)若CD = 3,AB + BC = 16,求△ABC的面积。

答案：
解:
(1)如图,BD即为所求.

(2)如图,作DH⊥AB于点H.
∵ BD平分∠ABC,DC⊥BC,DH⊥AB,
∴ CD=DH=3,
∴ △ABC的面积=$S_{\triangle BCD}+S_{\triangle ABD}=\frac {1}{2}BC\cdot CD+\frac {1}{2}AB\cdot DH$
$=\frac {1}{2}×3BC+\frac {1}{2}×3AB=\frac {1}{2}×3(BC+AB)=\frac {1}{2}×3×16=$24.

11. 求证：两个角及第三个角的平分线对应相等的两个三角形全等。

答案：
已知:如图,在△ABC和△A'B'C'中,∠A=∠A',∠B=∠B',CD,C'D'分别是∠ACB和∠A'C'B'的平分线,且CD=C'D'.
求证:△ABC≌△A'B'C'.
　　
证明:
∵ ∠A=∠A',∠B=∠B',
∴ ∠ACB=∠A'C'B'.
∵ CD,C'D'分别是∠ACB和∠A'C'B'的平分线,
∴ $∠DCB=\frac {1}{2}∠ACB,∠D'C'B'=\frac {1}{2}∠A'C'B'$,
∴ ∠DCB=∠D'C'B'.
在△DCB和△D'C'B'中,$\left\{\begin{array}{l} ∠B=∠B',\\ ∠DCB=∠D'C'B',\\ CD=C'D',\end{array}\right. $
∴ △DCB≌△D'C'B'(AAS),
∴ BC=B'C'.
在△ABC和△A'B'C'中,$\left\{\begin{array}{l} ∠A=∠A',\\ ∠B=∠B',\\ BC=B'C',\end{array}\right. $
∴ △ABC≌△A'B'C'(AAS).

12. 阅读下列解题过程并完成相应的任务。
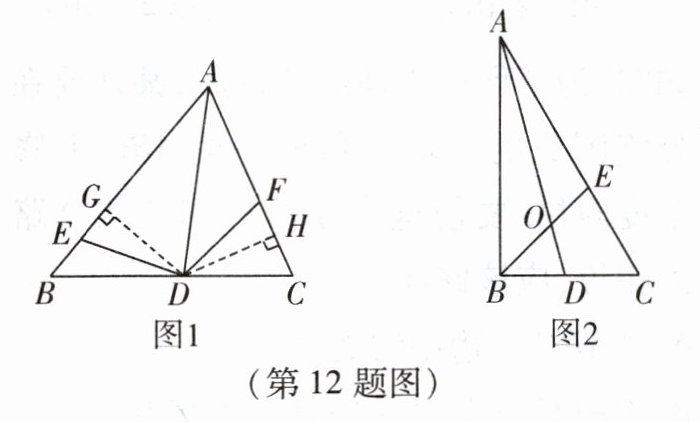
题目：如图1,在△ABC中,AD是∠BAC的平分线,点E,F分别在边AB,AC上,∠AED = ∠CFD。
求证：DE = DF。
证明：如图1,作DG⊥AB,DH⊥AC,垂足分别为G,H,根据角平分线的性质,得DG = DH。
……
反思：遇到和角平分线有关的题目,可以尝试向角的两边作垂线来寻求解题思路。
(1)补充题目中的解答过程。
(2)任务：如图2,在Rt△ABC中,∠ABC = 90°,∠C = 60°,AD,BE两条角平分线相交于点O。求证：OE = OD。

答案：
证明:
(1)在△DEG和△DFH中,$\left\{\begin{array}{l} ∠GED=∠HFD,\\ ∠EGD=∠FHD,\\ DG=DH,\end{array}\right. $
∴ △DEG≌△DFH(AAS),
∴ DE=DF.
(2)如图,过点O分别作OM⊥BC,ON⊥AC,OG⊥AB,垂足分别为M,N,G,连接OC.

根据角平分线的性质可知OG=ON,OM=OG,
∴ OM=ON=OG,∠OMD=∠ONE=90°.
∵ 在Rt△ABC中,∠ABC=90°,∠ACB=60°,
∴ ∠BAC=30°.
∵ AD是∠BAC的平分线,
∴ $∠DAB=\frac {1}{2}∠BAC=15^{\circ }$,
∴ ∠BDA=90°-∠BAD=75°.
∵ BE是∠ABC的平分线,∠ABC=90°,
∴ $∠OBM=\frac {1}{2}∠ABC=45^{\circ }$,
∴ ∠NEO=180°-∠EBC-∠ECB=180°-45°-60°=75°,
∴ ∠NEO=∠MDO.
在△OMD和△ONE中,$\left\{\begin{array}{l} ∠MDO=∠NEO,\\ ∠OMD=∠ONE,\\ OM=ON,\end{array}\right. $
∴ △OMD≌△ONE(AAS),
∴ OE=OD.