《2025年辽宁作业分层培优学案八年级数学上册人教版》

9. (锦州期末)在物理学中,过入射点垂直于镜面的直线叫作法线。光线在镜面上反射时,反射光线与法线的夹角和入射光线与法线的夹角相等。如图,两束光线 $ l_1 $,$ l_2 $ 分别从不同方向射向镜面 $ m $,入射点为 $ A $ 和 $ B $,$ n_1 $,$ n_2 $ 为法线,$ l_1 $,$ l_2 $ 的反射光线相交于点 $ P $。若 $ \angle 1 = 25^{\circ} $,$ \angle 2 = 45^{\circ} $,则 $ \angle APB $ 的度数是(C)

A.$ 60^{\circ} $
B.$ 65^{\circ} $
C.$ 70^{\circ} $
D.$ 75^{\circ} $

答案： C

10. 如图,已知 $ \angle BOF = 120^{\circ} $,则 $ \angle A + \angle B + \angle C + \angle D + \angle E + \angle F $ 为(D)

A.$ 360^{\circ} $
B.$ 720^{\circ} $
C.$ 540^{\circ} $
D.$ 240^{\circ} $

答案： D

11. 已知三角形的两边长分别是 4 和 6,则第三边中线 $ x $ 的取值范围是 1 ＜ x ＜ 5。

答案： 1 ＜ x ＜ 5

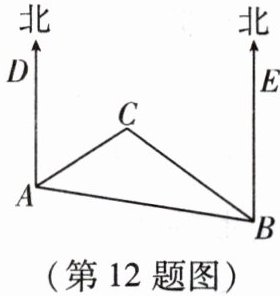
12. 如图,$ C $ 岛在 $ A $ 岛的北偏东 $ 50^{\circ} $ 方向上,在 $ B $ 岛的北偏西 $ 60^{\circ} $ 方向上,$ A $ 岛在 $ B $ 岛北偏西 $ 80^{\circ} $ 方向上,则从 $ C $ 岛看 $ A $,$ B $ 两岛的视角 $ \angle ACB $ 为 110°。

答案： 110°

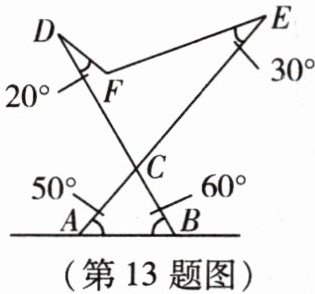
13. 如图是可调躺椅示意图(数据如图),$ AE $ 与 $ BD $ 的交点为 $ C $,且 $ \angle A $,$ \angle B $,$ \angle E $ 保持不变。为了舒适,需调整 $ \angle D $ 的大小,使 $ \angle EFD = 110^{\circ} $,则图中 $ \angle D $ 应减少 10 $ ^{\circ} $。

答案： 10

14. 如图,点 $ D $ 是 $ \triangle ABC $ 的边 $ BC $ 上任意一点,点 $ E $,$ F $ 分别是线段 $ AD $,$ CE $ 的中点,且 $ \triangle ABC $ 的面积为 40,则 $ \triangle BEF $ 的面积 = 10。

答案： 10

15. 如图,在 $ \triangle ABC $ 中,$ AE_1 $,$ BE_1 $ 分别是内角 $ \angle CAB $、外角 $ \angle CBD $ 的三等分线,且 $ \angle E_1AD = \frac{1}{3} \angle CAB $,$ \angle E_1BD = \frac{1}{3} \angle CBD $；在 $ \triangle ABE_1 $ 中,$ AE_2 $,$ BE_2 $ 分别是内角 $ \angle E_1AB $、外角 $ \angle E_1BD $ 的三等分线,且 $ \angle E_2AD = \frac{1}{3} \angle E_1AB $,$ \angle E_2BD = \frac{1}{3} \angle E_1BD $；…。以此规律作下去,若 $ \angle C = m^{\circ} $,则 $ \angle E_n = $ $\frac{m}{3^{n}}$度。

答案： $\frac{m}{3^{n}}$

16. (6 分)如图,$ AB // CD $,直线 $ EF $ 分别交 $ AB $,$ CD $ 于点 $ E $,$ F $,$ \angle BEF $ 的平分线与 $ \angle DFE $ 的平分线相交于点 $ P $,求证：$ \triangle EPF $ 是直角三角形。

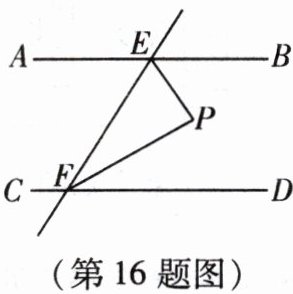
答案： 证明:
∵AB//CD,
∴∠BEF+∠DFE=180°.又
∵EP,FP分别平分∠BEF,∠DFE,
∴∠PEF=$\frac{1}{2}$∠BEF,∠PFE=$\frac{1}{2}$∠DFE,
∴∠PEF+∠PFE=$\frac{1}{2}$(∠BEF+∠DFE)=$\frac{1}{2}$×180°=90°,
∴△EPF是直角三角形.