《2025年辽宁作业分层培优学案八年级数学上册人教版》

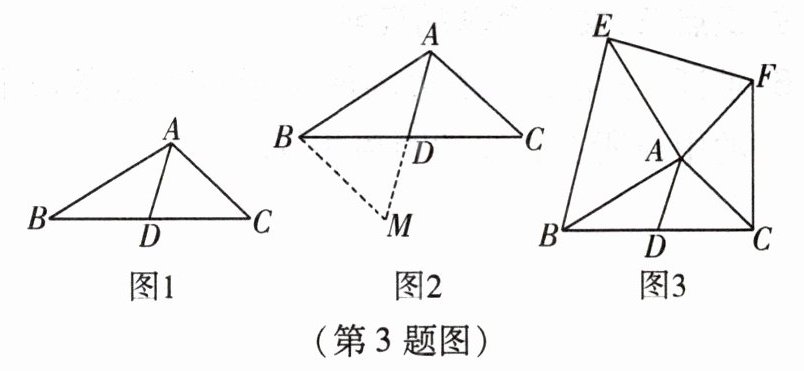
3. (1) 数学兴趣小组活动时,张老师提出了如下问题:如图 1,在△ABC 中,AB = 8,AC = 6,求 BC 边上的中线 AD 的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图 2):①延长 AD 到 M,使 DM = AD;②连接 BM,通过三角形全等把 AB,AC,2AD 转化在△ABM 中;③利用三角形的三边关系可得 AM 的取值范围为 AB - BM ＜ AM ＜ AB + BM,从而得到 AD 的取值范围是______.
上述方法我们称为“倍长中线法”. “倍长中线法”多用于构造全等三角形和证明边之间的关系.
(2) 请你写出图 2 中 AC 与 BM 的数量关系和位置关系,并加以证明.
(3) 如图 3,AD 是△ABC 的中线,AB = AE,AC = AF,∠BAE = ∠CAF = 90°,请直接利用(2)的结论,试判断线段 AD 与 EF 的数量关系,并加以证明.

类型四:半角模型

答案：
3.
(1)1＜AD＜7
(2)AC//BM,且AC=BM,
证明:
∵AD是△ABC的中线,
∴BD=CD.
在△MDB和△ADC中,BD=CD,∠BDM=∠CDA,DM=DA,
∴△MDB≌△ADC(SAS),
∴∠M=∠CAD,AC=BM,
∴AC//BM.
(3)EF=2AD.
证明:如图，延长AD到M,使DM=AD,连接BM.

由
(2)知AC=BM,AC//BM,
∴∠BAC+∠ABM=180°.
∵∠BAE=∠FAC=90°,
∴∠BAC+∠EAF=180°,
∴∠ABM=∠EAF.
∵AC=AF,
∴BM=AF.
在△ABM和△EAF中,AB=EA,∠ABM=∠EAF,BM=AF,
∴△ABM≌△EAF(SAS),
∴AM=EF.
∵AD=DM,
∴AM=2AD,
∴EF=2AD.

4. 在几何图形中,共顶点处的两个角,其中较小的角是较大的角的一半时,我们称之为半角模型. 截长补短法是解决这类问题常用的方法.
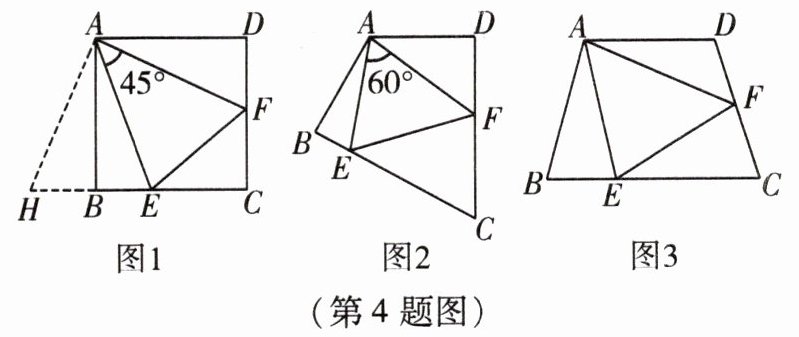
如图 1,在正方形 ABCD 中,以 A 为顶点的∠EAF = 45°,AE,AF 与 BC,CD 分别交于 E,F 两点,为了探究 EF,BE,DF 之间的数量关系,小明的思路如下:如图 1,延长 CB 到点 H,使 BH = DF,连接 AH,先证明△ADF≌△ABH,再证明△AHE≌△AFE. 从而得到 EF,BE,DF 之间的数量关系.
(1) 提出问题:EF,BE,DF 之间的数量关系为______.
(2) 如图 2,AB = AD,∠B = ∠D = 90°,以 A 为顶点的∠BAD = 120°,∠EAF = 60°,AE,AF 与 BC,CD 分别交于 E,F 两点,你认为(1)中的结论还成立吗? 若成立,请写出证明过程;若不成立,请说明理由.
(3) 如图 3,在四边形 ABCD 中,AB = AD = a,BC = b,CD = c. ∠ABC 与∠D 互补,AE,AF 与 BC,CD 分别交于 E,F 两点,且∠EAF = $\frac{1}{2}$∠BAD,求△EFC 的周长. (用含 a,b,c 的式子表示)

答案：
4.
(1)EF=DF+BE
(2)成立.
证明:如图1,延长CB到点G,使BG=DF,连接AG.

在△ABG和△ADF中,AB=AD,∠ABG=∠D,BG=DF,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠FAD.
∵∠EAF=60°,∠BAD=120°,
∴∠BAE+∠DAF=60°,
∴∠BAE+∠GAB=60°,
∴∠EAG=60°=∠EAF.
在△AGE和△AFE中,AG=AF,∠EAG=∠EAF,AE=AE,
∴△AGE≌△AFE(SAS),
∴GE=EF.
∵GE=BG+BE,
∴EF=DF+BE.
(3)解:如图2,延长CB到点H，使BH=DF,连接AH,

则∠ABH+∠ABC=180°.
∵∠ABC与∠D互补,
∴∠ABC+∠D=180°,
∴∠ABH=∠D.
在△ABH和△ADF中,AB=AD,∠ABH=∠D,BH=DF,
∴△ABH≌△ADF(SAS),
∴AH=AF,∠HAB=∠FAD.
∵∠EAF=$\frac{1}{2}$∠BAD,
∴∠BAE+∠DAF=∠EAF,
∴∠BAE+∠HAB=∠EAF,
即∠HAE=∠FAE.
在△AHE和△AFE中,AH=AF,∠HAE=∠FAE,AE=AE,
∴△AHE≌△AFE(SAS),
∴HE=EF.
∵HE=HB+BE,
∴EF=DF+BE,
∴△CEF的周长为CF+EF+CE=CE+CF+BE+DF=CB+CD=b+c.